Introduction to Perps
Levana Well-funded Perps is a protocol for perpetual swaps, which are leveraged trading contracts. It aims to manage risk and provide benefits to both traders and liquidity providers.
For traders, Levana's solution is to make all positions "well-funded," meaning that the maximum profit for each position is locked in advance. This eliminates the possibility of bad debt and insolvency, providing greater security.
Liquidity providers, on the other hand, receive a yield for taking on the risk of market instability. They supply funds that act as collateral, and in return, they earn a fee with a risk premium.
The protocol addresses the issues with existing perpetual swap models, such as the virtual AMM. These models rely on complex mechanisms to maintain price stability, but they have limitations and can be risky in volatile markets.
By separating different trading pairs and creating a decentralized market for liquidity, Levana reduces the risk of contagion between different markets. This also makes it easier to expand to other blockchain networks.
Overall, Levana's perpetual swaps protocol offers a reliable and secure platform for traders and liquidity providers. It ensures fair settlement, minimizes risks, and allows for the development of additional financial protocols on top of tokenized positions.
Glossary of Terms
The following is a glossary of terms commonly used throughout the rest of the documentation. It pairs very well with the high level overview. If this is your first time reading about Levana Perps, some of the concepts below may not make sense on first read. Our recommendation for getting up to speed is to:
- Review this page, not getting hung up on concepts that don't make sense
- Go through the high level overview, referring back to this page to check definitions
- Review the slides
- Come back to this page; the terms should make much more sense at that point
- Base asset: the asset being speculated on. In a hypothetical ATOM/USD perps market, ATOM would be considered the base asset.
- Quote asset: the currency used for denoting the price of the base asset. We are speculating on the price shift between base and quote assets. In the ATOM/USD case, USD would be the quote asset.
- Collateral asset: the asset deposited into the perps system by both traders and liquidity providers. Due to the implementation of crypto-denominated pairs, this could be either the base or quote asset.
- Notional asset: the opposite of the collateral asset. In the ATOM/USD market, if ATOM is used as collateral, USD is the notional. The concept of notional asset is an internal implementation detail of the platform; traders will generally want to think in terms of base and quote. This is also explored in more detail in crypto-denominated pairs.
- Entry price: price of the asset at the time a position was opened. From a user perspective, price is always given in quote-per-base units (e.g. 10 USD per ATOM). Internally it will also be represented as notional-per-collateral.
- Deposit collateral: the total amount of collateral asset deposited by a trader to open a position.
- Counter collateral: the amount of collateral locked from the liquidity pool in a position.
- Max gains: the maximum amount of gains a trader can achieve on a position. Unlike other platforms, Levana perps’ well-funded guarantees rely on having locked maximum gains for a position.
- Note that max gains are not exposed in the UI, instead we use a take profit price for user convenience.
- Leverage: how much to leverage your collateral when opening a position. Positive leverage means taking a long position and negative means taking a short position.
- Notional size: the overall size of a position. This is the deposit collateral times leverage. It is stored in terms of the notional asset, and is converted to collateral using the entry price. Note that positive notional size is a long position and negative is a short position.
- Net notional: the sum of the notional size of all open positions. A positive net notional means that longs are more popular than shorts and therefore longs will pay a funding payment to shorts.
- Delta neutral: when the net notional in the protocol is 0, meaning an equivalent value of longs and shorts are open. We strive to keep the protocol delta neutral to protect liquidity providers from price exposure risk.
- Trading fee: fee paid by traders when opening or updating positions. This is split between the protocol and liquidity providers following the protocol tax config value. By default, 30% goes to the protocol, 70% goes to LPs.
- Delta neutrality fee: a fee paid when an action moves the protocol away from delta neutral, and received when an action moves the protocol towards delta neutral. For example, if longs are more popular than shorts, opening a long will incur paying out a fee, and opening a short will receive a payment from the delta neutrality fund.
- Borrow fee: fee paid by traders to liquidity providers for locking up liquidity. The fee is split between the protocol and LPs using the same protocol tax as the trading fee uses. This is an ongoing fee collected on a continuous basis as long as the position remains open.
- Active collateral: the amount of collateral available within a position. This will start off equivalent to deposit collateral minus fees paid at position open. However, as additional fees are paid and price movements are adjusted for, the active collateral will go up or down. Note that this will change the effective leverage of a position, since the notional size will remain fixed.
- Liquidation price: the price at which a position will be force-closed because it risks being insolvent and unable to pay additional fees. This can occur because the price has moved or because fees have depleted the active collateral.
- Take profit price: the price at which a position has achieved its maximum possible PnL by capturing all the counter collateral locked in the system. At this point, the position is force-closed and profits delivered to the user.
- Liquifunding: a process performed when positions are updated, closed, and on a regular basis to collect fees, adjust balances for price exposure, and determine new liquidation prices.
- Liquifunding delay: the time period of delay between a position being opened/updated/liquifunded and the next scheduled liquifunding.
- Staleness period: The time interval that a position can remain open after the completion of the liquifunding delay without risking illiquidity. If a position remains open past this period, the protocol is considered stale.
- Notional size in collateral (previously called notional value): This is the notional size of the position converted to the collateral asset at the current exchange rate.
- Liquidation margin: funds set aside within a position’s active collateral that can cover the maximum potential fees the position can occur until its next “staleness” point. If the position if not liquifunded before that staleness point, the entire protocol becomes stale since we cannot guarantee well fundedness.
- Position size: exposure to the base asset of the position.
- Carry leverage: the amount of leverage we assume cash-and-carry traders would use for balancing the market. This setting is present to ensure we leave sufficient liquidity for balancing positions.
Levana Well-funded Perpetuals - high level overview
This document provides a high level overview of the Levana Well-funded Perps (hereafter: perps or Levana perps) system. It is intended to be read by people already familiar with the general concept of perpetual swaps platforms, and will focus on the distinguishing characteristics.
You may want to first review the glossary.
- The problems we're solving
- The solutions
- Crypto denominated pairs
- Liquifunding
- Price updates
- Cranking
- Staleness
- Congestion
- Price triggers
- Liquidity pool
The problems we're solving
Levana Perps started from trying to solve a fundamental problem common in other perps platforms: the risk of illiquidity. In most perps platforms, traders going long are betting against traders going short. When the price moves upward, long positions take profits from short positions, and vice-versa. If longs and shorts remain balanced within the platform, then each side has sufficient liquidity to guarantee their profits.
However, as we have seen historically, this assumption of balanced markets is not always met. This is especially true in extreme market conditions, such as a market meltdown. In such a case, we may see far greater short positions than longs, and the protocol may be unable to honor profits for those positions due to insufficient liquidity.
Solving this problem drives the majority of the unique features within Levana perps. Keeping this risk in mind will help you understand why the protocol works the way it does.
A secondary issue we strive to address is market manipulation. In tradition vAMM/mark price perps platforms, position entry and exit prices are based on a mark price within the protocol. When there is low volume within the protocol, it becomes easier for traders to significantly move the mark price, allowing them to force-liquidate counter-traders and extract profits risk-free. Our design attempts to make Levana Perps a protocol that works for both a low volume perps protocol, and for smallcap coins, as well.
The solutions
There are two fundamental shifts in Levana perps versus traditional perps platforms
Locked liquidity
Instead of longs and shorts taking profits from each other and risking illiquidity, the protocol introduces the concept of liquidity providers (LPs). LPs provide assets that can be locked by traders against their positions. That locked liquidity represents the maximum gains a trader can achieve on a given position. Markets can be created in both stablecoin and crypto-denominated pairs. Crypto-denominated pairs have no capped gains for long positions. Stablecoin denominated pairs include capped gains to ensure all positions are fully collateralized at all times. Capped gains is a downside versus other perps platforms (but see crypto-denominated pairs for a mitigation), but ensures that all positions are, at all times, fully collateralized.
Additionally, the introduction of LPs into the protocol provides a relatively low-risk (though not risk-free) method for passive income.
Another advantage to having fully collateralized, well-funded positions is that it obviates the need for off-chain liquidation bots. Alternative perps platforms must make use of high availability, off-chain services to perform just-in-time liquidations in order to keep illiquidity to a minimum. In contrast, Levana perps is able to perform on-chain liquidations, thereby reducing its reliance on external services.
No mark price
Levana perps does not maintain an internal mark price concept. Instead, the spot market price is used for entry price and calculation of PnL within the system. This allows the protocol to remain stable even with little internal volume. It also avoids issues found with the more common vAMM approach to mark price perps, such as needing to choose an initial mark price and drifting further away from it as the spot price changes over time.
Funding payments are still used to encourage cash-and-carry arbitrage to balance out the protocol. However, instead of being based on a mark/spot price divergence, funding payments are now based on the net notional or total difference in long vs short position sizes.
Additionally, Levana perps introduces a concept called a delta neutrality fund to further incentivize a balanced protocol. Unlike funding payments, the delta neutrality fund takes lump-sum payments at position open, update, and close. Actions that push the protocol closer towards neutral receive a payment from the fund, and actions that push the protocol away from neutral pay into the fund.
Crypto denominated pairs
In addition to the problems described above, Levana perps attempts to address two additional issues:
- We would like to support chains that do not have easy access to reliable stablecoins. In such chains, a trading pair like ATOM/USD would generally be difficult for users to interact with due to lack of access to a USD-denominated coin.
- The limitation on capped max gains via stablecoins may limit use cases for some traders that would prefer to realize infinite gains on their positions, crypto-denominated pairs enables this.
To address both points, we introduce the concept of a “crypto denominated pair.” The underlying mechanism we use for such crypto denominated pairs is a "collateral-is-base" market, which is described further in our slides. By contrast, a stablecoin-denominated market would be called "collateral-is-quote."
In a “collateral-is-quote” perps market, the base asset (e.g. ATOM) is priced in terms of the quote asset (e.g. USDC), and traders deposit USDC to trade.
In a crypto-denominated pair, we flip this around. From a user perspective, we still talk about ATOM and USD as base and quote, respectively. However, the user deposits ATOM instead of USD. This addresses point 1: Levana perps can host a trading pair on a chain so long as either the base or quote assets are supported on that chain.
The second point requires a bit more of an explanation.
Infinite max gains
Suppose we have a stablecoin based market for ATOM/USDC. The trader wants to open up a long position on ATOM. The trader will:
- Establish an entry price, let’s say 10 USDC per ATOM
- Deposit some amount of collateral, let’s say 200 USDC, equivalent to 20 ATOM
- Set a max gains and lock some counter collateral from the liquidity pool. Let’s say this is 400 USDC. This establishes a max gains for the trader on this position of 200% (they deposited 200 USDC and could maximally walk away with 600 USDC, taking a 400 USDC profit).
Now, instead, let’s consider the situation where the trader is interacting on a market with ATOM as collateral, not USDC:
- Instead of depositing 200 USDC, the trader deposits 20 ATOM
- Similarly, instead of locking 400 USDC from the liquidity pool, the trader locks 40 ATOM
In such a case, the maximum collateral the trader can walk away with is 60 ATOM (20 deposit collateral + 40 counter collateral). This would appear initially to be the same as the 600 USDC described in the stablecoin market scenario.
However, PnL is not denoted in terms of ATOM. Instead, PnL is denoted in terms of the quote asset, or in this case USD. Since the trader opened a long position, the value of the collateral (ATOM) will continue to rise as long as the price rises.
In this case, the trader would like to tell the protocol to simply not provide a max gains price and allow a position to remain open regardless of how high the price goes. This would allow the trader to realize infinite profits in terms of USD. The protocol therefore allows a setting of “infinite max gains”, which skips the max gains price.
Note that this is only possible with long positions in markets where the base asset is used as collateral. When the quote asset is used as collateral, or for short positions, infinite gains are not possible.
Flipped leverage
The public interface of the system speaks about base and quote almost exclusively. Traders denote their leverage in terms of base (e.g. ATOM). Internally, the system works almost exclusively in terms of the notional and collateral assets. In essence, the system behaves as if the trader is depositing collateral to speculate on price movements of notional.
For traditional markets where base is notional and quote is collateral, this all lines up as expected. For example, with ATOM/USDC, the trader deposits USDC and opens a long position, hoping that the price of ATOM relative to USDC goes up. The system sees this as a long position with positive leverage.
However, in a crypto-denominated market like ATOM/USD, we turn all of this around. The collateral is now ATOM, and therefore the notional asset is USD. Internally, the protocol views everything as speculation of the price of USD in terms of ATOM. To understand how flipped this is, consider this table:
| Standard ATOM/USD | Inverse price USD/ATOM |
|---|---|
| $10/ATOM | 0.1 ATOM/USD |
| $16/ATOM | 0.0625 ATOM/USD |
| $8/ATOM | 0.125 ATOM/USD |
As the price of ATOM goes up, this is equivalent to the price of USD relative to ATOM going down, and vice-versa. Therefore, opening up a long position on ATOM is equivalent to opening up a short position on USD.
When receiving an order to open a position from a trader, the protocol accepts the leverage value in terms of the base and quote assets. It then converts that leverage number depending on whether collateral is base or quote. In a “standard” collateral-is-quote setup, the leverage is unchanged. In a “flipped” collateral-is-base setup, a long leverage is converted to short and vice-versa.
Complex side point: the simplest way to do this conversion is to simply negate the number: a 5x long position on ATOM becomes a 5x short position on USD. This turns out to introduce non-linear gains, because the trader is still exposed to price movements of ATOM by holding onto some ATOM as collateral. Instead, the formula we use is leverage-in-quote = 1 - leverage-in-base to account for that exposure. Therefore, if the trader opens a 5x long in a flipped market, internally this turns into a 4x short, or a leverage-in-notional of -4. This is discussed in more detail in our slides.
Liquifunding
When a position is open, we calculate a number of parameters for the position. We first deduct the trading fees and any payments to or from the delta neutrality fund from deposit collateral. Then, we determine the maximum amount of fees the position may incur over the next period of time (the liquifunding delay plus staleness period) and set that aside as the liquidation margin. We then determine, based on the remaining active collateral, at what price point the position would become illiquid (the liquidation price) and when it would have achieved maximum gains (the max gains price). We set these values in liquidation data structures to be used by cranking. We also schedule a next liquifunding to occur after liquifunding_delay.
Later, the position will be liquifunded, either because of cranking or because the user attempts to update or close the position. At this point, the protocol needs to calculate how many fees and funding payments have been incurred since the last liquifunding and update active collateral. It also updates active collateral to reflect price exposure, meaning changes resulting from price movements. If the price moves in the direction of the position, active collateral goes up, otherwise it goes down.
NOTE Following on our well-funded concept: each position has locked counter collateral from the liquidity pool. When active collateral goes up due to price movement, the counter collateral goes down in the same amount, and vice-versa.
We then perform the liquidation margin calculation again. If there are insufficient funds for a liquidation margin, the position is closed. If max gains have been achieved, the position is closed. Otherwise, the new parameters are updated, new liquidation and max gains prices are set for cranking, and a new next liquifunding is scheduled.
NOTE: an interesting side-effect of the active collateral changing from liquifunding is that the leverage of a position will change over the course of its lifetime. The leverage will go down as the price moves in the direction of the position and funding payments are received. The leverage will go up as the price moves against the position and funding payments and borrow fees are paid.
Price updates
The protocol receives price updates via a permissioned entrypoint in the protocol. This entrypoint delivers the current price of the base asset in terms of the quote asset. The protocol stores this in a collection of previous price points and then performs a crank.
Note that the address approved to set the price can either be a wallet or a smart contract. Using a wallet essentially means that a trusted backend service will directly update oracle price into the market. By contrast, if the chain Levana perps is running on hosts a trusted third-party oracle, a smart contract solution can be deployed which will query the current price from the oracle and submit it to the perps contract. This allows the perps protocol to remain agnostic to where prices come from, and proactively perform tasks on a push-basis of prices being injected, rather than needing a pull-based model for querying for new prices.
In practice, production deployments of Levana perps currently all use the Pyth price oracle for price data, and a companion pyth_bridge contract acts as the permissioned price admin. This setup allows anyone to permissionlessly update the price in the Pyth oracle (using cryptographic proofs from the Pyth network) and then trigger the pyth_bridge to update the market with the new price.
Cranking
The crank process is responsible for running scheduled tasks and performing tasks (like closing liquidatable positions) based on price triggers. Cranking works by going through all price updates and performing operations for each price update point:
- Looks for any positions with a scheduled liquifunding in the past and performs the liquifunding process on it
- Looks for any positions with price triggers that are hit by the new price update. For example, if a long position has a liquidation price of $7 and a price update sets the price to $6, the position should be closed as liquidated.
After all actions are taken for the given price update, the crank sets the “last crank complete” to the timestamp of that price update and continues.
Once all liquifundings are completed and we have caught up to the latest price point, the protocol does not require any cranking. A query endpoint is available to check if crank work is available, and bots run regularly to perform cranking when work is available. In the future, we intend to provide incentivization for third parties to run crank bots.
Note that cranking is a permissionless process. It also involves some other corner-case maintenance activities on the protocol, like market wind-down "close all positions" and resetting LP balances on full liquidity withdrawal. However, these aren't core to the understanding of the system.
Staleness
The protocol relies on timeliness on two fronts:
- Price updates. If price updates are blocked to the system (such as by DDoS attacking an oracle), an attacker would be able to open a position based on knowing with certainty the current spot price and its discrepancy from the last price update in the system.
- Example: suppose the current price of ATOM is $10, and an attacker suspects the price will rise to $15. The attacker could simply open a long position, but that incurs risk that the price could actually go down. Instead, the attacker DDoS attacks the oracle, preventing any price updates into the system. The attacker can then observe the real movement of the spot price. If, as expected, the price moves to $15, the attacker can then open a long position (locked into the last price update of $10) and halt the DDoS attack on the oracles, allowing the protocol to see the new $15 price and realizing a large profit.
- Liquifunding. Liquifunding is the process that ensures that all open positions have sufficient liquidation margin to cover potentially incurred fees. If we go beyond the staleness period of a position, it may become insolvent, breaking our well fundedness goals.
To address both concerns, the protocol introduces the concept of staleness. If a price update has been delayed for too long a period, or if any position has reached the point where liquidation margin cannot be guaranteed, we become stale. When stale, the protocol will not allow positions to be opened, updated, or closed, or limit orders to be placed. To exit a stale period, price updates must come into the system and/or cranking be performed.
Under normal conditions, with a functioning blockchain, functioning oracle, and functioning crank bots, the protocol should never reach staleness. This is an extreme condition that indicates something has broken and the protocol needs to protect traders and liquidity providers.
Congestion
Congestion is similar in behavior to staleness, but derives from a different source. Consider this sequence of events:
- Price is updated in protocol to $8, and the crank is fully run.
- Price is updated to $9, but the crank does not fully run because of a large number of liquifundings.
- Price is updated again to $10, but the crank still hasn't finished processing the $9 price update.
- A trader opens a long position at the (correct) entry price of $10, and ends up with a liquidation price of $9.
- The crank finally moves past the liquifundings for the $9 price update in (2) and begins running price triggers (liquidations, take profit, etc.). It sees that the position opened in (4) should be liquidated at the price of $9 and closes it out.
This last step is a bug. The position had an entry price of $10, and that price landed after the $9 price we're currently cranking. We should not liquidate positions based on old prices.
To address this, we have the "pending price triggers" queue. If our crank ever falls behind on a price update, we place new positions' trigger prices on a queue and only add them to the price trigger tables after liquidations for that entry price have been fully processed. The downside of this queue is that the work items for opening and updating positions are doubled: we now need both a transaction to open/update the position, and another one to crank the position's price trigger to pop it from the "pending price triggers" queue and move it to the price trigger tables.
A potential attack vector would be forcing the protocol to fall behind on cranking (such as by DDoS attacking the crank bots) and then flood the system with open and update position messages, causing a large stream of work for the crank. An attacker could continuously update existing positions to keep putting them back onto the queue, causing the crank to never fully catch up.
To mitigate this, we introduce the concept of congestion. Once the pending queue reaches a certain size (by default, 500), we disallow opening or updating positions.
Like staleness, under normal circumstances this situation should never arise. However, by providing a congestion mechanism, we prevent any bug in the system or attack on the system from spiraling out of control.
Price triggers
The protocol automatically determines a liquidation and max gains price for a position at each liquifunding. Additionally, a user may set trigger prices for stop loss and take profit to avoid complete liquidation or to take profits early. These price triggers are observed by the crank mechanism, and positions are closed. Note that if a liquidation price hits before a stop loss, or a max gains hits before a take profit, the liquidation or max gains prices will be used.
Liquidity pool
A core feature of Levana perps is locked liquidity, which is provided by the liquidity pool. A liquidity provider can deposit collateral into the pool and receive LP tokens in exchange. These LP tokens can be burned to receive back collateral. If there is insufficient collateral available, the liquidity provider will need to try to withdraw liquidity later.
Instead of receiving LP tokens, liquidity providers can opt to receive xLP tokens. These xLP tokens cannot be immediately burned for collateral. Instead, xLP can be converted into LP tokens. This is a time-based conversion process that occurs linearly over 45 days. In other words, if you unstake 450 xLP tokens, after the first day you’ll have 10 LP tokens available, after the second day 20, and so on. Providers are rewarded with higher rates of return, and the protocol benefits by having more gradual liquidity withdrawals, making it less likely that there will be no available unlocked liquidity.
LP and xLP token holders receive pro-rata portions of the trade and borrow fees paid by traders. As mentioned above, xLP token holders will receive higher portions overall as an incentive.
The utilization ratio within the protocol is the percentage of collateral in the liquidity pool that is currently locked to a position. The higher the utilization rate, the higher the borrow fee will be. This provides a free-market incentive structure for setting the borrow fee naturally. If the borrow fee is too low, providers will not deposit collateral, leading to a higher utilization rate and higher fees. If the fee is too high, more providers will deposit collateral, leading to a lower utilization rate and lower fees.
The goal of the protocol is to protect providers from market movements. There are essentially two kinds of market movements that present a risk to liquidity providers:
Normal market movement
Under normal market movement conditions, the price moves in a “reasonable” timeframe up and down. The risk to liquidity providers is that, when a trader opens a position, the LPs are essentially forced to take an opposite side position. To make that concrete, consider a situation where everyone anticipates a 5% rise in the price of ATOM. Traders will flock to the system, opening large numbers of long positions, and liquidity will be locked as counter collateral. That counter collateral will be lost if the market goes up, essentially meaning LPs are taking a short position.
The problem here is that the longs far outweigh the shorts. If, instead, there was an equal amount of short and longs (i.e., the protocol’s net notional was balanced, a.k.a. we were delta neutral), LPs would face no risk: a positive price move would lose LPs money on the long positions, but would make back equivalent money on the short positions.
To protect LPs, the protocol has two mechanisms in place:
- Like most perps platforms, funding payments incentivize arbitrageurs to open cash-and-carry positions. If longs are more popular than shorts, an arbitrageur can open a short position in the perps platform, receive funding payments, and simultaneously open a long position in the spot market. The arbitrageur is now neutral on price movements, but receives a funding payment regardless. Similarly, assuming the presence of an external platform supporting shorts (e.g., a traditional options market), the arbitrageur can counter the protocol being overly short by opening long positions and opening short positions externally.
- The protocol introduces the concept of the delta neutrality fund. As the protocol veers further and further away from delta neutral, actions that exacerbate the imbalance will pay a fee into the fund, and actions that bring the protocol closer to neutral receive a payment from the fund. At the extreme, delta neutrality capping will prevent opening new positions or updating existing positions. (Closing positions is always allowed, even if it pushes the protocol further beyond the caps.)
- Note that, to prevent price manipulation attacks from being successful, we charge a tax (by default, 5% for most markets) on payments into the delta neutrality fund. This means that, even if an attacker could manipulate the spot price of an asset, each iteration of draining liquidity from the protocol would involve losing a portion of the profits to the delta neutrality fund. The 5% tax number increases the more susceptible an asset is to spot price manipulation (e.g., low spot volume coins will have a higher tax).
️️⚠️ Normal market risks
WARNING: Liquidity providers are subject to a real risk of impairment, where the value of their LP and xLP tokens in terms of the underlying collateral asset may go down over time. This will occur if the market is imbalanced and traders are successful overall. (By contrast, if the market is imbalanced and traders are unsuccessful in their trades, liquidity providers will benefit.) Liquidity providers can judge their exposure to this risk by observing the net notional, or the difference between long and short open interest. If there are more longs, liquidity providers will experience impairment if the price goes up, and if there are more shorts, they will experience impairment if the price goes down.
Delta neutrality ratio is another helpful parameter to look at. It reflects the price exposure risk of liquidity pool relative to its size. It is calculated at net notional divided by liquidity pool size. This will effectively express that as the size of the pool increases, the impact of a constant-size net notional imbalance will be reduced.
As the Levana Perps platform grows over time, cash-and-carry activity will yield higher rewards and net notional is expected to move closer to 0 (a neutral platform). During the bootstrapping phase of the protocol, there is expected to be more volitility and therefore more risk. The natural mechanism for addressing this is higher borrow fees from liquidity pool utilization that is higher than target utilization, which will reward providers for their assumed risk (and impairment losses) with higher APRs.
Extreme market movement
While normal market price movements are mostly addressed by the above mitigations, extreme market conditions are not. This is the primary risk undertaken by liquidity providers. Consider a case where the price of an asset collapses from $120 to $0.01. While that may seem extreme, one could imagine a scenario where that could happen.
In such a situation, we can assume that traders would stop opening long positions and would all try to open short positions. Pretty soon, delta neutrality caps would prevent further short positions from being opened, so we would be left with a market with some longs and lots of shorts. The longs would likely attempt to close their positions, which is allowed even in the presence of delta neutrality capping. We would now be left with a protocol almost 100% weighted towards shorts.
At this point, liquidity providers would likely be concerned for their investment and would attempt to burn their LP tokens, freeing their liquidity. Unfortunately, there will not be enough unlocked liquidity for all the providers trying to withdraw their liquidity. So we’ll be left with a significant portion of liquidity locked as collateral on short positions, essentially forced to take long positions that they cannot exit.
As the meltdown occurs, the short positions will begin to achieve max gains and capture the entirety of the counter collateral. In a crypto-denominated market, the risk asset itself is becoming worthless, but liquidity providers were prevented from selling the asset by the protocol. But in a stablecoin denominated market, the liquidity provider’s stablecoin is still valuable, and they have lost virtually all of it.
This is the risk liquidity providers need to be aware of when depositing in pools: in a market meltdown (or, equivalently, in a meltup) their deposited collateral can be almost entirely lost. Therefore, more volatile markets should demand a higher borrow fee to compensate for the increased risk assumed.
Position size versus locked collateral
One of the defining features of Levana Perps is locked collateral. This is the mechanism by which we ensure that each position's potential gains are well funded at all times. This can lead to some confusion about two similar but distinct topics: position size and max gains. We'll try to clarify that here.
NOTE: This document will intentionally use simplifying assumptions to make the math a bit easier, such as describing a collateral-is-quote market. If you try the same numbers in a collateral-is-base market—which includes any USD-denominated market—the numbers will be slightly different. But that shouldn't impact the intuition discussed here.
What is position size?
Position size represents how much exposure to price movement your position has. It is given by your deposit collateral times leverage. For example, if you deposit $500 in a long position and use 3x leverage, your exposure is equivalent to buying $1500 of the asset on the spot market. If the price goes up by 10%, you will make $150 in profit, not $50.
NOTE: This also explains why all leveraged positions have a liquidation price. In the above example, if the price went down by 50%, the position would have lost $750, which is more than the $500 the trader deposited initially. Therefore, we need a liquidation price that stops a position from losing more money than the deposit collateral. In this case, that would be a 33% price decrease. This also explains why the more heavily leveraged a position, the sooner you'll be liquidated if the price moves against you.
Position size is what determines open interest and net interest in the platform:
- Long open interest is the sum of the position sizes of all longs.
- Short open interest is the sum of the position sizes of all shorts.
- Total open interest is the sum of long and short open interest.
- Net open interest is the difference between long and short open interest.
What is locked collateral?
When you open a position, you specify a take profit price. Internally, the system converts this into a max gains, representing the maximum amount of profit you can ever take from this position. This occurs by borrowing liquidity from liquidity providers and locking it against your position.
Let's use the example above again. You have a long with a $1500 position size. The current price is $10. You set a take profit price of $12, or a 20% price increase. That means your max gains are $1500 * 20% == $300. The protocol needs to borrow those $300 from the liquidity pool and lock it into your position. This is the locked collateral, or equivalently the counter side collateral.
By constrast, if you reduce your take profit price from $12 to $11, the protocol only needs to lock collateral for $1500 * 10% == $150. Notice that the position size remains the same in both cases, but the locked collateral is significantly different.
As you can see in this example, the closer the take profit price is to the entry price, the smaller the locked liquidity. This is one of the reasons we recommend traders think carefully about the take profit prices they want. Not only is this a risk mitigation mechanism, but it is also a cost savings. Reducing your locked liquidity will reduce both your trading fees and your borrow fees.
Price risk to liquidity providers
Let's continue with the above example. A trader opens a long with the parameters:
| Parameter | Value |
|---|---|
| Deposit collateral | $500 |
| Leverage | 3x |
| Entry price | $10 |
| Take profit price | $12 |
The system will derive the following from these parameters:
| Derived parameter | Value |
|---|---|
| Trader position size | $1500 |
| Locked collateral | $300 |
Any gain the trader takes on the position will be withdrawn from the locked collateral, and vice-versa. Meaning, if the price moves up to $11:
- The trader has experienced a 10% increase via price exposure
- The trader will have profits of
$1500 * 10% == $150 - The liquidity pool will lose those $150 to the trader
- Caveat: as we discuss below, we strive to keep the protocol balanced, which will protect liquidity providers from these losses by ensuring for every loss on a long position, they will experience an equivalent gain on a short position, and vice versa.
Similarly, if the price decreases by 10% instead, the trader will lose $150 to the pool. This is equivalent to saying that, every time a trader opens a long, it's as if the liquidity providers have opened a short of the same position size. This leads to one more concept: counter-side leverage. In our example, the liquidity pool opened a $1500 short position using $300 of collateral. This means that the pool's counter-side leverage on this position is 5x, versus the trader's 3x leverage. From the liquidity pool's perspective:
| LP parameter | Value |
|---|---|
| Locked collateral | $300 |
| Counter side leverage | 5x |
| Position size | $1500 |
Why net open interest matters
The reason why net open interest is so important to the protocol is because it represents exposure to price risk for liquidity providers. If the protocol has too much long interest, for example, liquidity providers are being forced to open up more short positions than long positions. If the actual price goes up, liquidity providers will lose funds to traders through impairment. It's true that if the price moves down instead, liquidity providers will instead make money through impairment. But we strive to insulate providers from risk. Therefore, our goal is to keep longs and shorts balanced, also known as:
- 0 net notional
- Delta neutral
The mechanisms we use for this are incentives via funding rate payments and delta neutrality fees, which provide a profit motive for the implementation of cash-and-carry arbitrage, also known as basis trading.
Collateral lock-ups, risks and rewards
The inherent risk liquidity providers take on in this system is unbalanced price exposure. While—as just discussed—the protocol strives to minimize that risk, it cannot guarantee risk will be absent. And furthermore, in extreme market conditions (called a market meltdown or meltup), this risk is expected to be very high. In such a scenario, any liquidity in the pool is at risk of impairment, up to loss of 100% of their funds.
Liquidity providers can choose their level of risk, and receive commensurate rewards as a result. Therefore, there are two mechanisms for providing liquitity: LP tokens with no lock-up time, and xLP tokens with a 45 day lock-up window. LP tokens can be immediately withdrawn, provided that enough liquidity is in the system. xLP holders take on a higher degree of risk, and therefore receive higher rewards in terms of receiving a higher proportion of trade and borrow fees.
But to be clear, both groups are at risk of significant impairment. The protocol uses a dynamic borrow fee rate detection mechanism within the protocol to allow supply-and-demand forces to discover a fair market rate for this risk, a mechanism discussed in much more detail in our whitepaper. But the summary is: for assuming the risk of extreme market movements, LP and xLP holders are rewarded with high APRs on their deposits.
More details
This document attempts to focus on just the question of position size versus locked collateral. There is more information available in the rest of the doc site which may be relevant:
- High level technical overview
- The explainer slides give many more examples. The liquidity pools, trading overview, and collateral is base decks will be especially relevant.
Levana Well-funded Perpetuals Whitepaper
- Abstract
- 1. Motivation
- 2. High level protocol overview (TODO: better drawings)
- 3. Trading Mechanics
- 4. Incentivization structure
- 5. Liquidity Providers
- 6. Delta Neutrality Fee
- 7. Liquidations
- 8. State Staleness and Cranking
- 9. Crypto denominated markets and off-chain notional
- 9.1. Delta-neutral staking rewards arbitrage strategy
- 9.2. Long positions staking rewards propagation as negative funding rates
- 9.3. Stablecoin denominated pair with off-chain notional index
- 9.4. LP’s yield on crypto tokens in crypto denominated pairs
- 9.5. Settlement of crypto denominated pair trading position equivalence
- 10. Risks, rewards, guarantees and fee size
Abstract
Levana Well-funded Perps is a leveraged, well-funded and collateral-settled perpetual swaps protocol. It introduces a novel way to delineate risk between market participants. The incentive structure offers risk premium to the liquidity providers taking on the spot market illiquidity risk. Some of its key features are:
- Strong guarantees for settlement: Traders get strong guarantees for settlement in any future market conditions with a very low liquidation margin ratio. Liquidation price is solely based on spot price feed.
- Risk premium for liquidity providers: Liquidity Providers receive a risk premium for taking on spot market meltdown risk. This yield is found in a free market of supply and demand for liquidity to be used as collateral.
- No risk fund: Protocol doesn’t require a risk fund and the DAO Treasury has no insolvency risk.
The absence of native price discovery in spot-price settled perps is addressed by introducing a Capped Delta Neutrality Fee mechanism.
1. Motivation
1.1. Problems with constant-product virtual AMM model
A popular model for perpetual swaps is the constant-product virtual AMM (vAMM). This model introduces a virtual market against which users can trade. To ground it in reality and keep the virtual market’s price (known as the mark price) in line with the spot price, the protocol relies on a special payment referred to as a funding payment. This payment incentivizes traders to balance out long/short interest and keep the price stable.
This design was innovative and allowed for a perpetual swaps DEX to exist without an order book. However, it has critical flaws that prevent it from functioning long term in anything but a calm, low volatility market.
At the core of these flaws lies the fact that the vAMM model has unfunded liabilities. To pay out the profits to a particular trader, the vAMM model depends on two things:
- Liquidating other trader’s positions before they go into bad debt.
- Ensuring that certain positions remain open to keep the mark price close to the spot price.
This problem is usually solved with high liquidation margins, a reliance on off-chain liquidation bots, capital controls (such as disallowing withdrawals, closing and delisting markets, etc.), and heavy-handed dynamic fee incentives in the form of uncapped and sensitive funding rates. While these solutions work to mitigate some of the problems, they do not address the core issue, which is accentuated by the fact the protocol must still maintain an imbalance of open interest.
The magnitude of the imbalance is equal to the notional size of a position that would move the vAMM price from the price it was initiated at to the current spot price. This imbalance generally grows with time, especially in a market meltdown or melt-up. The initial vAMM price can be moved, but it is very costly to the protocol and doesn’t work in a meltdown scenario.
As the imbalance grows, so does the protocol’s unfunded liabilities. The protocol simply owes more to the popular side than it has locked in from the unpopular side. At this point, a race scenario is created whereby traders on the popular side are incentivized to close their positions quickly to ensure that they realize all of their profits. As the protocol is drained, it accrues bad debt and heads towards insolvency.
The vAMM model is brittle and has an open interest imbalance risk reminiscent of an algorithmic stablecoin depeg risk. Piling up additional incentives or market participants on a fundamentally flawed model does not inspire confidence. Because of that, Levana went back to the drawing board to design a leveraged perpetual swaps financial model that is well-funded as a core principle.
1.2. Benefits of Well-fundedness
A trader’s unrealized profit is a liability to the protocol. That liability is well-funded when the maximum profit is locked for specifically that position. By making all positions well-funded, the protocol gains the following benefits:
- Traders are guaranteed a fair settlement payout in any market conditions.
- Bad debt is impossible for a position by construction.
- Without bad debt, there is no risk of insolvency to the protocol as a whole.
- There is no rush to perform liquidations just-in-time before the position goes into bad debt.
The collateral that is locked as maximum profit comes from liquidity providers. Liquidity providers take on the risk of spot market meltdown. For taking on this risk, they receive a borrow fee with a risk premium.
The benefits of this mechanism are:
- This mechanism creates a decentralized supply-and-demand free market for liquidity with yield denominated in the collateral asset.
- The protocol does not have to rely on inflationary token emissions to attract liquidity.
- Different listed trading pairs are completely separated from each other with their own liquidity markets. This ensures that there is no contagion risk between different markets.
- Having completely independent markets makes deploying cross chain simple, as there is no risk fund or basket of notional assets that needs bridging.
- Well-fundedness guarantees to traders’ positions enable fearless composability of other financial protocols on top of tokenized positions.
2. High level protocol overview (TODO: better drawings)
Levana Well-funded Perps is a platform for leveraged perpetual trades. It has multiple completely separate listed markets, each of which is a trading pair of a notional index and a collateral crypto asset.
A trader that wishes to enter a position provides collateral and gains leveraged exposure to the notional index price. All traders are guaranteed to be able to close their positions, settling with the oracle spot price. The oracle spot price is the current exchange ratio between the notional index and collateral asset.
Markets are generally separated into two categories: stablecoin denominated and crypto denominated:
- A crypto denominated market has US dollars as the notional asset and a volatile native or bridged asset as the collateral asset in which every trade is opened and settled. Crypto denominated markets are well-suited for native to chain crypto assets and bridged assets with deep liquidity. Trading pairs with native crypto collateral assets do not have stablecoin depeg, centralization or bridge hack risks, and create sought-after crypto-asset lending with fair risk-premiums.
- A stablecoin denominated market has a stablecoin set as its collateral asset and any notional index. Stablecoin denominated pairs are well-suited for small-cap crypto assets that are not bridged to the platform’s chain and off-chain assets. These trading pairs make it possible to list any exotic, non-crypto, or synthetic asset and create delta-neutral stablecoin lending with fair risk-premiums.
2.1. Trader’s position
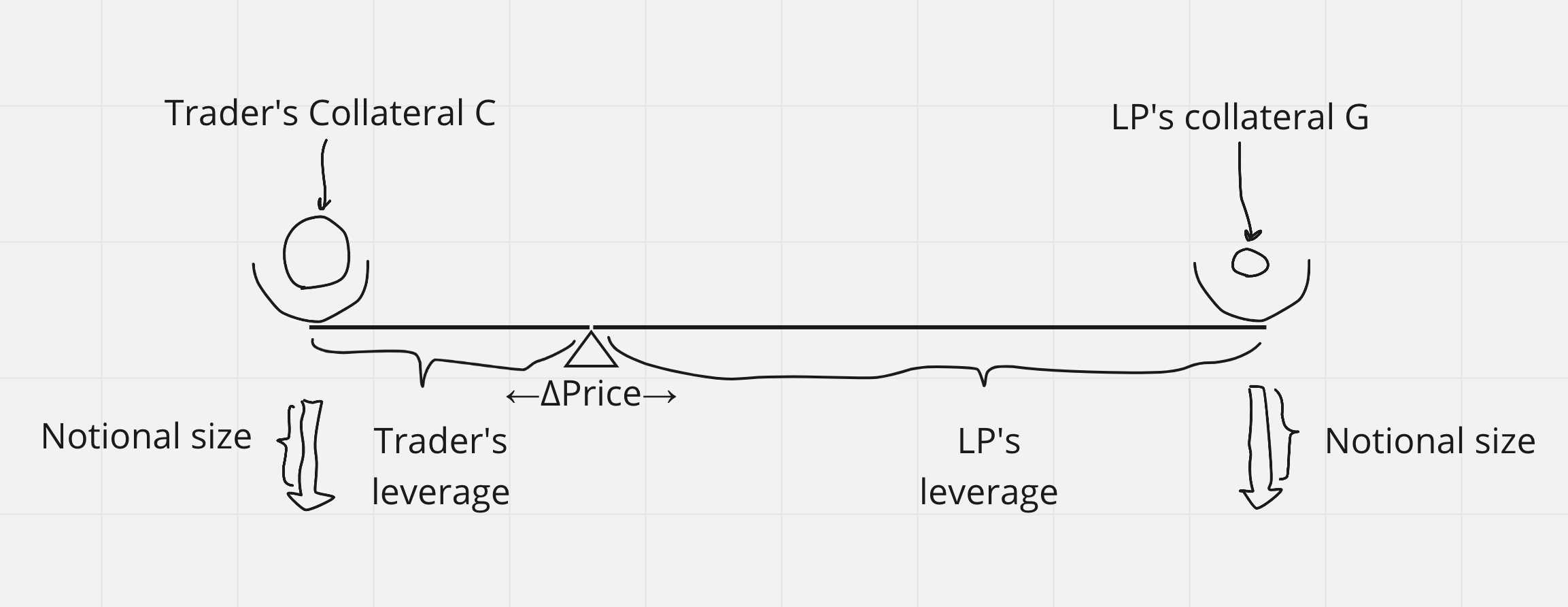
Figure 1. Leveraged position on Levana Well-funded Perps. TODO: notional size arrows should be reverse of each other. Add fee arrow directions.
Traders open positions by providing collateral and choosing position parameters. In a crypto denominated pair, the traded crypto asset itself acts as collateral, while in the stablecoin denominated pair, that stablecoin acts as collateral.
Position parameters are:
- Leverage of the trade. Leverage and provided collateral (with entry price) define the notional size.
- Max gains that this position can realize. This defines the amount of collateral that will be locked on the counter-position of the trader’s position. Long positions in a crypto denominated trading pair have an option of infinite max gains.
💎 Internally, Levana Perps uses max gains to define how much counter collateral to lock against a position. However, the web frontend does not expose this concept. Instead, it exposes the more familiar concept of a take profit price. The frontend is responsible for calculating the amount of max gains necessary to ensure the specified take profit price.
The collateral that the trader provides defines the max loss to the trader. The collateral that the protocol locks in the counter-position defines the max profit to the trader.
In a crypto denominated pair, long positions may have unlimited max profit if the locked collateral for the counter-position is equal in size to the whole notional size of the position.
Max loss of a position is realized when the oracle price feed crosses a liquidation price threshold. Similarly, max profit is realized when the oracle price feed crosses a take profit price, if present.
Traders may close their position at any point in time, settling the payouts to themselves and Liquidity Providers at the current spot price.
💎 All positions in Levana Perps are well-funded. Well-fundedness is a guarantee to settle at any time, at any spot price, and in any market conditions.
A trader may be unable to open a new position that would use more collateral on the counter-side than the liquidity remaining in the pool of available capital. This is expected to happen only in extreme market conditions.
2.2. Liquidity Providers’ pool of capital and yield
Liquidity Providers deposit their funds into a single pool of capital denominated in the collateral asset of the trading pair. This pool is specifically for that trading pair, and funds from it are used to enter into a net total counter-position to all traders’ positions for that trading pair.
To make the liquidity pool roughly delta-neutral with respect to the notional index, the protocol charges a per-block funding rate fee from owners of popular-side positions and pays this to owners of unpopular-side positions. The payment is scaled with signed notional size of the position.
To compensate Liquidity Providers for the cost of their capital and a premium on the risk that they take on, the protocol charges a per-block borrow fee from all traders and pays it to Liquidity Providers as yield on provided principal.
🔥 Liquidity Providers take on the risk of the meltdown (or melt-up) of the assets, but not a bear (or bull) market. The difference between meltdown and a bear market of the same magnitude is the existence of cash-and-carry traders comfortable enough to perform arbitrage to earn funding rate payments, bringing the LP pool into rough delta-neutrality.
2.3. Protocol Market Participants and Incentives schema
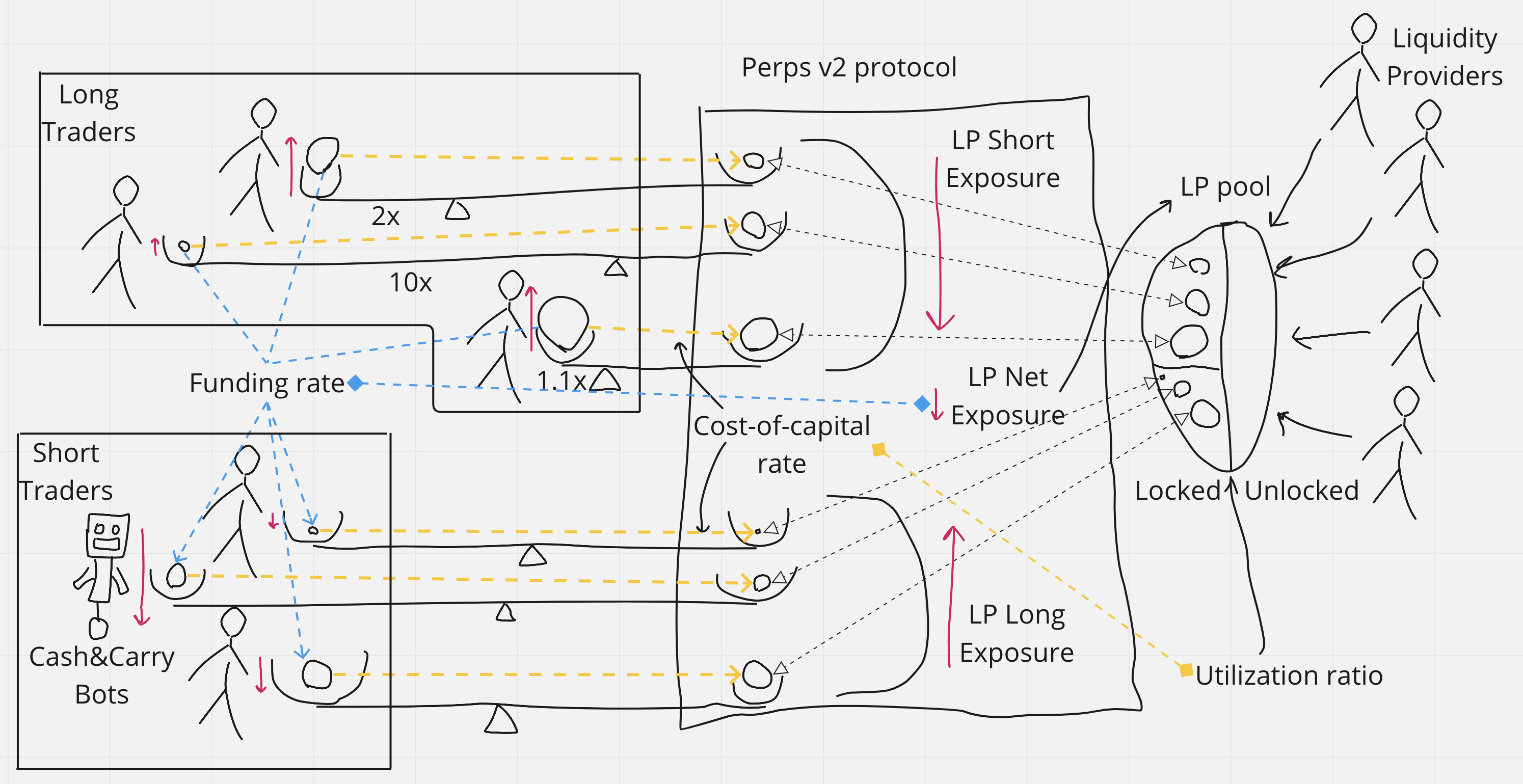
Figure 2. Market participants and protocol balancing on Levana Well-funded Perps. TODO: Borrow fee yellow lines should go into a separate yield fund, not collateral on the counter-side. Add delta neutrality fund to the schema?
Funding payments are paid from positions with popular directional exposure to the unpopular ones. The funding rate is scaled with net notional open interest. The funding payment for a particular position is scaled with notional size of that position.
Cash-and-carry bots come to earn funding payments. To do that, they open unpopular positions on Levana Well-funded Perps, and also open counter-positions on the spot market to become delta-neutral.
For crypto denominated pairs with collateral assets that have high staking rewards, there is also a unique delta-neutral strategy available on Levana Perps that allows traders to earn staking rewards without exposure to the underlying asset. This possibility exists because it is possible to open a short position that pays a borrow fee on a fraction of the notional size of the position.
Liquidity Providers pool their capital into a single liquidity fund per market. This pool of funds is used to lock collateral on the counter-sides of all traders’ positions. The fund has a utilization ratio of locked funds to all funds in the pool. Borrow fee payments are payed for locked collateral on the counter-side and appear as yield for Liquidity Providers. A part of the yield stream goes to the protocol treasury.
2.4. Protocol dynamics listing a high staking rewards token
The unique feature of Levana Perps is that traders pay a borrow fee on counter-side collateral, which can be multiple times lower than the notional size of the position. This gives traders the ability to hedge high staking reward tokens cheaply, making it viable to earn delta-neutral yield from staking.
Because the delta-neutral strategy opens short positions on Levana Perps, funding rates will persistently pay long position holders to hedge the shorts. Funding rates would become a cut-down version of staking rewards, paid on leveraging up the notional size of long positions. This allows token bulls to both be able to enter a long leveraged position and still receive at least a portion of the staking rewards without having to decide on one or the other.
Liquidity Provider’s yield is found in the supply and demand dynamics, and would most likely end up being the risk-free staking rewards yield, plus the risk premium perceived by LPs.
All three types of actors: delta-neutral arbitragers, token bulls, and LPs - have unique and attractive use cases in Levana Perps, which enable each other.
3. Trading Mechanics
3.1. Opening a new position
On opening a new position, the trader provides the position parameters and sends funds with trading fees. If the conditions to open a new position are met, the position is opened and a guarantee is made to the trader.
3.1.1. Open message parameters
Open message for a new position \(pos\) with oracle price of a particular trading pair contains three parameters:
- — notional size of the position. This parameter does not change until the position closes or the trader explicitly updates . is positive if trader’s side of the position is long and negative if it is short.
- — Collateral on trader’s side of the position .
- — Collateral on counter-side of position . Also known as max profit on position .
The position is opened with oracle price feed:
- — exchange price of notional index to collateral asset at ’s open transaction timestamp.
3.1.2. Funds and trading fees on opening a position
During the execution of the open message, funds and fees are transferred:
- amount of collateral from a trader’s deposit account is locked.
- amount of collateral from unlocked pool of LP capital is sent and locked in a locked pool of LP capital .
- An NFT token representing trader’s side of the position is minted and sent to the trader.
- A trading fee (default ) of notional size denominated in collateral is sent into Yield Fund.
- A trading fee (default ) of counter-side collateral is sent into Yield Fund.
- A delta neutrality fee is paid to or received from the delta neutrality fund . See Section 6 for more details.
3.1.3. Conditions for opening a new position
To successfully open a position, these conditions should be met:
-
Leverages on traders side and on counter-side should not exceed maximum allowed leverage (default 30x) of the trading pair.
-
Open message fails if the delta neutrality cap is reached and opening a position would have pushed open interest into further imbalance.
-
Open message fails if it is not possible to bring open interest back into balance without either closing existing positions or having more liquidity provided. More precisely, message fails if the rest of unlocked LP capital leveraged up at is not enough to balance net open interest imbalance :
-
If utilization ratio hits close to 100%, traders may be unable to open new positions.
-
There must be sufficient unlocked liquidity in the protocol that a balancing position can still be opened after this action which would bring net notional to 0. We use the carry leverage parameter for this, which indicates the minimum counter leverage value necessary on a balancing position.
All market participants take on the risk of bugs and hacks of the protocol infrastructure:
- A bug in the implementation of the protocol.
- A hack of bridge of the collateral asset if it is a bridged asset.
- Oracle hack or downtime.
- Blockchain downtime removing the ability to execute message closing the position.
Now, let us dive into quantitative estimations of all these risks and rewards.
3.2. Settling an existing position
The trader may choose to close his existing position and settle at the current oracle price. There are no conditions that need to be met to settle the position, and the payout is always fair because the position is well-funded.
Let us consider the case where the position have not crossed liquidation price or take profit price. The case of settling the liquidated position is explained in Section 7.
Payout to the trader on settlement will be equal to:
Where:
- — price difference between price at the moment of settling and at the moment of open.
- — payout to LPs, will be sent to .
- — payout from (or to, if is negative) the delta neutrality fund on settling trade.
- — funding payment that was lazily accumulated, but was not yet actualized.
- — borrow fee payment that was lazily accumulated, but was not yet actualized.
More about fees and in Section 4. More about capped delta neutrality in Section 6.
The total amount of funds associated with the position and sent as payouts at settlement is:
Form that we can calculate LPs’ payout:
LP payout is not affected by funding payments or delta neutrality fee paid by the trader. Borrow fee payments are sent into a separate fund from which LPs are free to withdraw their share.
3.3. Updating Position
All three of the position main parameters , and can be updated after opening the position. The process is functionally equivalent to settling and immediately reopening a position with the new parameters. The only difference of update to that two-step process is trading fees. Trading fees are charged on the difference of new and old and .
This means that the protocol does not charge any trading fees at all to top up or withdraw collateral on the trader’s side. The fees on topping up to increase Take Profit price or slightly changing to target a desired leverage are efficient for the trader.
3.4. Tokenized positions
On opening position , the trader receives an NFT token representing the position . The owner of the token can update or settle the position. The original owner is free to sell their position on the secondary position market.
3.5. Peer-to-peer position
The positions on the protocol are symmetrical in terms of price movement and collateral. The asymmetrical parts are fees and the fact that only traders have the right to settle a position.
The symmetrical nature of the underlying financial instrument, well-fundedness of a position, and the tokenization of the position allow the position to be decoupled into a natively-leveraged peer-to-peer futures contract represented as a pair of interlinked NFTs. One NFT represents long side of the trade, and the other NFT represents the short side of the trade.
More information can be found in Section 10.
4. Incentivization structure
Protocol incentives are structured in such a way that:
- Traders are able to open new positions.
- The pool of funds from Liquidity Providers removes most risks, except for spot market illiquidity risk.
To meet these requirements, Levana Well-funded Perps has two capped dynamic fee mechanisms.
4.1. Fee rate cap
Traders’ existing positions do not depend on the protocol staying in balance. The only way that an unbalanced protocol state affects existing positions is through dynamic fees.
The protocol has reasonable caps on dynamic fee rates. This allows the protocol to uphold the spirit of the well-fundedness guarantee. Without a fee cap, in a market meltdown scenario, the fees may skyrocket, liquidating positions that should have been in major profit instead.
The protocol can afford to cap the fees because all positions are well-funded. Even if the protocol does not charge any fees, max loss and max gains are locked, so any price at settlement is funded.
4.2. Protocol Balance
Levana Well-funded Perps has two ways it can become unbalanced.
4.2.1. Long and short notional open interest imbalance
Net notional open interest is the total net exposure to the notional index of all opened positions. Liquidity Providers’ exposure to the notional asset is exactly opposite: . The protocol tries to maintain rough delta-neutrality for liquidity providers, so it tries to balance around .
The mechanism for balancing is a variation on a familiar concept: a funding fee payment from popular-direction positions to unpopular ones.
4.2.2. Balancing utilization ratio of Liquidity Providers’ pool of capital
Utilization ratio of LPs’ pool of capital is the ratio between capital that is locked as collateral in the counter-positions to traders and all the funds in LPs’ pool of capital.
The protocol has a target utilization ratio . If current utilization ratio deviates from , the LP pool becomes unbalanced. is chosen to be as close to as possible, but not so high that it would cause problems. A dynamic way to find appropriate is explained in Section 5.
- If is significantly lower than , then the capital efficiency of the provided liquidity is low. Only the locked part of the provided liquidity actually earns a borrow fee, but the yield is spread over all liquidity, locked and unlocked.
- If the utilization ratio is high and closing on , then traders are unable to open new positions and liquidity providers are unable to withdraw their funds because there are no unlocked funds available.
The mechanism to entice LPs to provide collateral is borrow fee payments that always flow from the direction of traders to LPs. The borrow fee rate is gradually updated such that the utilization ratio would stay at .
4.3. Fee payment
Fee payment is accounted for with nanosecond precision and retroactively calculated at the moment of payment. Each position makes fee payments regularly at its own cadence, or when it is updated or closed. This ensures that each position pays the fees exactly for every block that it was opened for.
The position liquidation margin includes just enough funds to cover one fund period's worth of funding payments for the position. This is necessary to ensure that positions on the unpopular side will receive all of the funding payments that they are due under any market conditions.
4.4. Funding rates and payments
Funding payments are done exclusively between positions. This means that the total amount charged as a funding payment from a popular position is the total amount received by the corresponding unpopular positions.
Usually, perpetual protocols have the same funding rate for popular and unpopular sides. This means that the total amount charged is always higher than amount sent as funding payments and the protocol pockets the difference.
As Levana Well-funded Perps is well-funded and does not have to cover bad debts, there is no need to pocket the difference. This means that the actual funding rates on the platform can be smaller.
Equality in total amounts of funding payments means that there will be two funding rates: one for longs and one for shorts.
4.4.1. Funding rates
Funding rates change only when positions notional sizes change, which means the protocol is able to update the funding rates data series and have all the per-block lazily calculated information about funding rates.
The popular side funding rate and effective funding rate sensitivity are defined per block as:
Now depending on which side is more popular the long funding rate and short funding rate are defined as
- Equal amount of longs and shorts ( is 0):
- = 0 or = 0 :
- Longs are more popular ( is positive):
- Shorts are more popular ( is negative):
Where:
- — total long open interest.
- — total short open interest.
- — total interest volume.
- — funding rate sensitivity parameter of the trading pair.
- — delta neutrality fee sensitivity parameter of the trading pair.
- — delta neutrality cap parameter of the trading pair.
- — maximum funding rate parameter of the trading pair, usually 90%.
4.4.2. Funding payment
With funding rates known for any block, it is possible to lazily calculate average funding rate over a specified time period .
With that, the funding payment is:
The payment amount has an upper bound:
Where:
- is either the take profit or liquidation price level, depending on whether is long or short.
4.5. Borrow fee rate and payments
The borrow fee is based on the supply and demand of the protocol’s liquidity. And the decision as to when users will provide liquidity to the pool, is made based on several factors. Liquidity providers provide liquidity to the pool if the borrow fee rate is high enough to cover risk-free potential yield and premiums for all of the perceived risks.
The borrow fee carries three functions:
- Risk-free potential yield passed up.
- Risk premium on notional or collateral asset meltdown/melt-up.
- Compensation for delta neutrality index having a small, but persistent bias.
All three functions can be covered by one mechanism that determines the borrow fee rate.
4.5.1. Borrow fee rate
Just as funding rates change per block, borrow fee rates also change per block, but gradually. The change in the borrow fee rate from the previous block to a new one is proportional to the difference between the target utilization ratio and the actual utilization rate in that block. More details can be found in Section 5.
4.5.2. Borrow fee payment
With a borrow fee rate known for the liquifunding period, the funding payment for a time period inside the liquifunding period can be calculated. Let's first consider the uncapped version of the borrow fee payment:
Where:
- — length of period of time in question.
- — average borrow fee rate over period .
- — average value of price multiplied by the borrow fee rate in that block over period .
Borrow fee payment has an upper bound, because is bound by :
5. Liquidity Providers
Liquidity Providers can provide collateral asset into an LP pool of a particular trading pair. For providing liquidity, the LP tokens are minted and signify a share of the pool.
Borrow fee payments are credited pro-rata to owners of LP tokens and stored in a separate Yield Fund alongside the trading fees. LPs are free to withdraw their per-block accumulated share of the yield fund. A fixed percentage of the Yield Fund is credited to the DAO Treasury.
Withdrawing from the liquidity pool is only possible if there is collateral left that is not locked into any counter-position.
5.1. Supply and demand for liquidity
Liquidity Providers offer liquidity to the system in the form of collateral ready to be locked into counter-positions. Traders create demand for that liquidity by locking counter-position collateral and not closing their old positions. The borrow fee rate is the price signal in that supply and demand dynamics.
If the borrow fee rate increases, it means that LPs earn a higher yield and traders pay higher fees. In this case, the supply of liquidity increases because LPs are attracted to earn higher yield, and the demand from traders decreases. The reverse is also true: if the borrow fee rate decreases, the supply decreases and the demand increases.
A gradual automatic borrow fee rate update mechanism allows the free market of liquidity to find an appropriate price for that liquidity.
5.2. Liquidity Provider pool utilization ratio
Liquidity Providers’ pool of capital has two parts: funds locked as collateral in counter-positions to all opened positions, and unlocked funds . Only actually collects a borrow fee from traders. This means that LPs’ pool at any time has the utilization ratio:
To target a specific utilization ratio, the borrow rate can be gradually changed. The target utilization ratio should be close to to make the LPs’ pool capital efficient, but not quite at so that there is plenty of collateral to allow new positions to be opened or some LPs withdrawing funds. A healthy utilization ratio is somewhere in the range of 75% to 90%, depending on the exact trading pair.
5.3. LP and xLP tokens
In addition to holding LP tokens, Liquidity Providers have an optional ability to time lock part of their LP tokens and mint xLP tokens. Minting xLP by burning LP tokens is immediate, but the reverse operation of time unlock happens gradually and linearly over a set and long period of time, such as 45 days, chosen per trading pair.
To incentivize time locking of LP into xLP, xLP tokens receive a higher proportion of fees than LP tokens. This is called the xLP rewards multiplier. Each market contains a configuration for a minimum and maximum xLP rewards multiplier (by default, 1 and 2, respectively). The actual value is chosen by interpolating between the low and high value based on the proportion of collateral deposited into LP vs xLP. For example:
- If all collateral is in xLP, no additional incentivization is needed, and the minimum multiplier is used.
- If all collateral is in LP, we need to maximize the incentivization, and the maximum multiplier is used.
- If the collateral is split 50/50 between LP and xLP, the midpoint between minimum and maximum is used.
Time lock on xLP with gradual and linear unlock into LP tokens allows to also change gradually and continuously. This, in turn, allows for gradual and continuous updating of the borrow fee rate.
5.4. Withdrawing Liquidity
Withdrawing liquidity associated with xLP tokens is made to be a long process by design. This leaves liquidity associated with LP tokens with more opportunity to withdraw in a market meltdown. But even so, of funds are targeted to be locked. In a market meltdown scenario, there may be an on-chain first-come first-serve race to withdraw unlocked funds. As the meltdown continues, we expect that:
- Traders will continue to drain liquidity from the pool.
- New traders will continue to enter the market, absorbing any unlocked liquidity available, essentially creating a liquidity race between traders and liquidity providers.
- Due to the fast nature of a meltdown, and the fact that we cap borrow fees, borrow fees paid to liquidity providers will be negligible compared to impairment losses.
- The utilization ratio will remain close to 100%, regardless of target utilization ratio, until all liquidity is drained.
This is the primary risk associated with being a liquidity provider. xLP holders absorb a higher portion of this risk because they have no ability to quickly exit their positions, even if unlocked liquidity is available.
One mitigation for this is providing secondary marketplaces for trading LP and xLP tokens directly. This also provides an automatic risk measurement indicating the perceived likelihood of a market meltdown playing out.
5.5. Borrow fee rate updating mechanism
With target utilization ratio and actual utilization ratio known at a per-block basis, it is possible to compute the average bias of the actual utilization ratio from target utilization ratio over the previous liquifunding period.
The borrow fee rate for the new block can be calculated as follows:
Where:
- — a meta-parameter, sensitivity of the borrow fee rate to utilization ratio bias.
A PID-controller choosing a new value based on signal may be appropriate to fine-tune and the differential and integral parameters.
6. Delta Neutrality Fee
Spot-price perpetual protocols without delta neutrality fee have no native price discovery mechanism. The model depends on arbitrage with the spot market to propagate the price response through the spot price oracle.
If the perpetual swaps volume starts to approach the volume on the spot market, big trades on the protocol without a delta neutrality fee would benefit traders at the expense of liquidity providers by creating small-scale flash meltdowns and meltups.
Spot market manipulation also starts to become more profitable. If an attacker is able to manipulate the spot market price short-term by a significantly higher margin than trading fees on the protocol, they are able to guarantee a profit from the protocol, ultimately draining liquidity providers.
To alleviate all of these problems, a delta neutrality fee (DNF) mechanism is introduced.
The cap on the delta neutrality fee rate is required to uphold the spirit of well-fundedness. If the protocol balance could make the delta neutrality fee arbitrarily large, the guarantee to traders to settle at any time and price would be compromised.
The DNF’s primary purpose is to defend liquidity providers. And, because DNF lowers risk to LPs, it lowers borrow fees. This is an additional benefit to traders, making a protocol with a DNF mechanism more attractive to both traders and LPs.
6.1. Delta neutrality fee construction
The delta neutrality fee is a percentage difference between the trade price and spot price, and it is directly proportional to the short-long open interest imbalance.
6.1.1. Instant delta neutrality fee
Instant delta neutrality fee at current net open interest is defined as:
Where:
- — clamped into the range .
- — sensitivity parameter of the trading pair.
- — cap parameter of the trading pair. A good default value is .
The sensitivity is chosen depending on the estimation of the price elasticity of the spot market, not the protocol itself. If the DNF on the protocol is at least times more elastic than on the spot market, the price signal can travel into the spot market. This means that, for markets with very deep liquidity (e.g., the bitcoin market), the DNF can in practice be made extremely small.
Because the price is chosen to be more elastic on the Levana Well-funded Perps market than on the spot market, traders who want to enter huge positions are incentivized by high DNF costs to split them into multiple positions, giving time for arbitrage to occur in between these sub-trades.
can be estimated by answering the question: How much new spot long interest is needed to double the price?
6.1.2. Delta neutrality fee of a trade
An open position, update position or settle position trade will experience a DNF proportional to the change to current net open interest resulting from the trade.
First, in case of the DNF being capped both before and after the trade, the total DNF for the trade on position would be:
Now, let’s consider a case where the trade does not hit a DNF cap and is positive. The DNF for the trade would be equal to the integral of the instant DNF over the change in net open interest:
For complex cases, it is possible to calculate the total DNF by splitting the trade into sub-trades that either stay capped or uncapped for the entire sub-trade.
Notice, that DNF of a position is denominated in notional index. Also notice that the DNF has an excellent property of impermanence. DNF on any set of trades with zero total net notional size change would incur zero total DNF.
6.2. Delta Neutrality Fund
The delta neutrality fund is a pool of funds that collects and pays out DNF on all trades on the platform.
6.2.1. Delta Neutrality Fund holding notional asset
Let us first consider a case in which the notional index is an actual crypto asset with a DEX trading pair between collateral and notional assets. The DNF incurred by trades can be collected and payed out denominated in that notional asset and stored in the Delta Neutrality Fund.
Because the DNF has a property of impermanence, it is exactly funded at any moment in time to pay out negative DNF on a set of trades that would bring to exactly zero. Let us call the ratio of the needed payout to the amount of funds in the delta neutrality fund, the fundedness ratio . It is always equal to if holds notional asset:
The DNF payouts on trades can now be seamlessly swapped using a DEX to allow traders to only ever provide and receive collateral asset. DEX trade slippage on DNF is charged to or sent from the trader to maintain at exactly .
If the DNF is so huge that the margin collateral is not enough to buy the required amount of notional asset, the fundedness would drop below . A way to process that state without failing is presented in the next section.
6.2.2. Delta Neutrality Fund holding collateral asset
Unfortunately, due to the property of impermanence, not all notional indices have on-chain asset and a deep liquidity DEX. In these cases, the fund may collect collateral asset instead of notional asset. This comes with the downside of floating .
for a trade is calculated as such:
- If is positive, meaning that DNF is charged from a trader, , the DNF payout value is the same and converted to collateral denomination using price at the time of the trade.
- This operation brings closer to in all cases.
- The cap on maximum DNF charged is kept, and well-fundedness guarantee to the trader is upheld.
- If is negative, meaning that DNF is payed out to a trader, , the DNF is additionally multiplied by fundedness ratio of the delta neutrality fund.
- This operation does not change .
- Payout to trader may be higher or lower depending on .
6.2.3. Fundedness ratio balance
The fundedness problem appears in the delta neutrality fund because it has liabilities denominated in notional asset but holds collateral asset. When the price changes, also changes.
By marking down (or up) all liabilities by the fundedness ratio, the delta neutrality fund is able to wind down and resets every time when changes sign.
Additionally, is expected to have a lot of churn. At every trade, either doesn’t change or closes to , applying pressure on the ratio to be near .
6.2.4. Maintaining fundedness ratio (WIP)
The delta neutrality fund may open a long notional position through as a trader, but with subsidised trading fees and DNF (but full funding and borrow fees). It would update its position every time a trade changes the balance of the delta neutrality fund to have all the funds as a collateral for the position with notional size . That way, the delta neutrality fund is able to maintain the fundedness ratio much closer to than when storing collateral directly.
6.2.5. Delta Neutrality Tax
One of the goals of Levana Perps is to support assets with overall lower trade volume. One added risk for such assets is lower capital requirements to manipulate the spot market price. Some such assets have the majority of their trade volume within AMMs, often on the same chain as the Levana Perps protocol itself. Such a situation can lead to an attack:
- Open a long position with Levana Perps
- Increase the price in the on-chain AMM via a large purchase
- Wait a few blocks for the manipulated spot price to be reflected through price oracles
- Close the long position and replace with a short position
- Decrease the price in the on-chain AMM via a large sell
- Close the short position and repeat the process
This attack can be successful if the profits achieved from Levana Perps outweigh the slippage and fees. This is not a zero-risk attack, since there may be other trades that intervene and reduce the delta neutrality fee profits. However, the risk is still high enough to be worth mitigating further.
One mitigation for this is delta neutrality fees and their sensitivity parameter, which will limit the amount of imbalance a trader can create during one of these attacks and thereby limit profits. However, with the Delta Neutrality Fee in place as described until now, there is inusfficient disincentive to an attack like this. It's true that the trader would make a large Delta Neutrality Fee payment when opening the initial long, but would immediately receive the full fee back on closing that long, assuming the attack is quick enough and does not give other traders an opportunity to balance the protocol.
As a further mitigation, we also introduce the concept of the Delta Neutrality Tax. This is a relatively small fee (suggested between 5% and 25%, depending on risk of spot price manipulation) which is taken from all payments into the Delta Neutrality Fund. With this tax in place and correct parameters chosen for caps and the tax, the attack described above will be unsuccessful, since:
- The caps limit the amount of total potential profit per spot price manipulation
- The tax directly reduces profitability by ensuring the trader receives less from the fund than paid into the fund
These tax payments are treated like trading and borrow fees, and are split between liquidity providers and the protocol using the protocol tax parameter.
6.3. Changing delta neutrality sensitivity
If , the delta neutrality fund is empty, and changing is a free action. If the delta neutrality fund has some non-zero amount of funds with fundedness , changing to will change that fundedness ratio. In this case, the amount of funds needed to be expended by the protocol to keep the same is:
It is actually very cheap, especially for markets with deep spot liquidity. For example:
- Bitcoin/dollar trading pair is listed and has open interest with imbalance of .
- Price sensitivity was estimated such that bitcoin market cap would change by per every of new open interest at market cap and , makes .
The cost to protocol to double sensitivity would be .
6.4. Comparison to Mark price from the constant-product model
Slipped spot price is reminiscent of the Mark price from the constant-product vAMM perp swaps model. They both present natively to the protocol's price discovery mechanism. But they have some core differences:
| Mark price (Constant-product vAMM model) | Slipped spot price (Well-funded Levana WFP) |
|---|---|
| Balances unfunded liabilities to traders | Protects LPs from spot market manipulators |
| Difference from spot price is uncapped | Difference from spot price is capped |
| Mark price sensitivity k is chosen to track protocol’s changing price elasticity | Slipped spot price sensitivity K_s is chosen as estimate to spot market price elasticity |
| k is very expensive to change | K_s is very cheap to change |
| Has permanent drift in the direction of peg price | Impermanent around current spot price |
| Stays the same on spot price changing | Changes with spot price maintaining the difference |
7. Liquidations
Traders’ positions have liquidation and take profit price levels. These prices slowly move over time due to funding payments being paid or received, and borrow fee payments being paid.
In the rest of this Section 7, the term “liquidation” is used for both liquidation of the trader’s side of the position as well as the forced take profit procedure on the trader. It may be thought of as liquidation of the counter-side of the trade.
Liquidation settlement of a position cannot happen automatically on reaching the liquidation price, so there is a period of time between the position satisfying liquidation conditions and the position actually settling.
There is no possibility of going into bad debt due to spot price movement, but that period of time is still problematic if it is not bounded. This is because the position contributes to the net notional position balance of the protocol, affecting funding rate and delta neutrality fees. In addition, it may have collateral locked in the counter-side, which affects the utilization ratio of the liquidity pool.
For that reason, a mechanism that checks for liquidatable positions is needed to periodically check-in on every opened position. The natural place for this is during funding payments, which already happen at regular intervals, referred to as the liquifunding period, for every open position.
Periodic check-ins bound the amount of time that a position can be left unsettled in a liquidatable state to one liquifund period. With that upper bound on the time, it is possible to calculate the maximum borrow fee and funding payments using fee rate caps.
By setting the margin collateral to that upper bound, the position is well-funded to pay out all fees incurred during the period of time it first became liquidatable up until the end of the liquifunding period. The trader is free to close the position in that period of time to avoid paying fee rates for that duration.
In addition to dynamic fee rate payments, the position may need to pay out a delta neutrality fee payment up to a cap. In practice, this would be the biggest contributor to the margin amount for most trading pairs.
7.1. Liquidation condition
First, the margin amount is defined as the max possible fees to be paid at the liquifunding period.
Next, the liquidation condition is the price going over the liquidation price level at which the amount of collateral becomes less than the margin amount.
Finally, the historical liquidatability check procedure is explained, which finds the first point of time at which the position becomes liquidatable.
7.1.1. Liquidation margin and condition without fees
If there were no fees (e.g. true for peer to peer positions), the margin amount would be exactly zero: , .
Where:
- — trader’s liquidation price.
- — trader’s take profit (max gains) price.
7.1.2. Liquidation margin
First, let’s calculate max delta neutrality fee that the trader may have to pay on liquidation:
Where:
- — upper bound on price at liquidation.
- — upper bound on delta neutrality fee payout.
Next, let’s calculate max funding and borrow fee payments and add it into total max fee :
Where:
- — upper bound on payout due to funding payment, borrow fee payment and delta neutrality fee.
- and — upper bounds on funding payment and borrow fee payment from Section 4.
is the margin collateral amount for the trader’s side. Counter-side margin collateral is still exactly , just like in the case without any fees, because all the fees are charged from the trader’s side.
7.1.3. Liquidation condition
From these lower bounds for the collateral at a price and margin collateral to be maintained, we can calculate the liquidation and take profit price levels:
7.2. Fee Periods and Liquidatability checking
With margin collateral and liquidation condition expressed as liquidation price , which is constant for the duration of a liquifunding period, let’s define the historical liquidatability check procedure.
The best way to understand the purpose of the liquidatability checking procedure is to look at a price chart with liquidation levels and liquifunding period start and end timestamps drawn down:
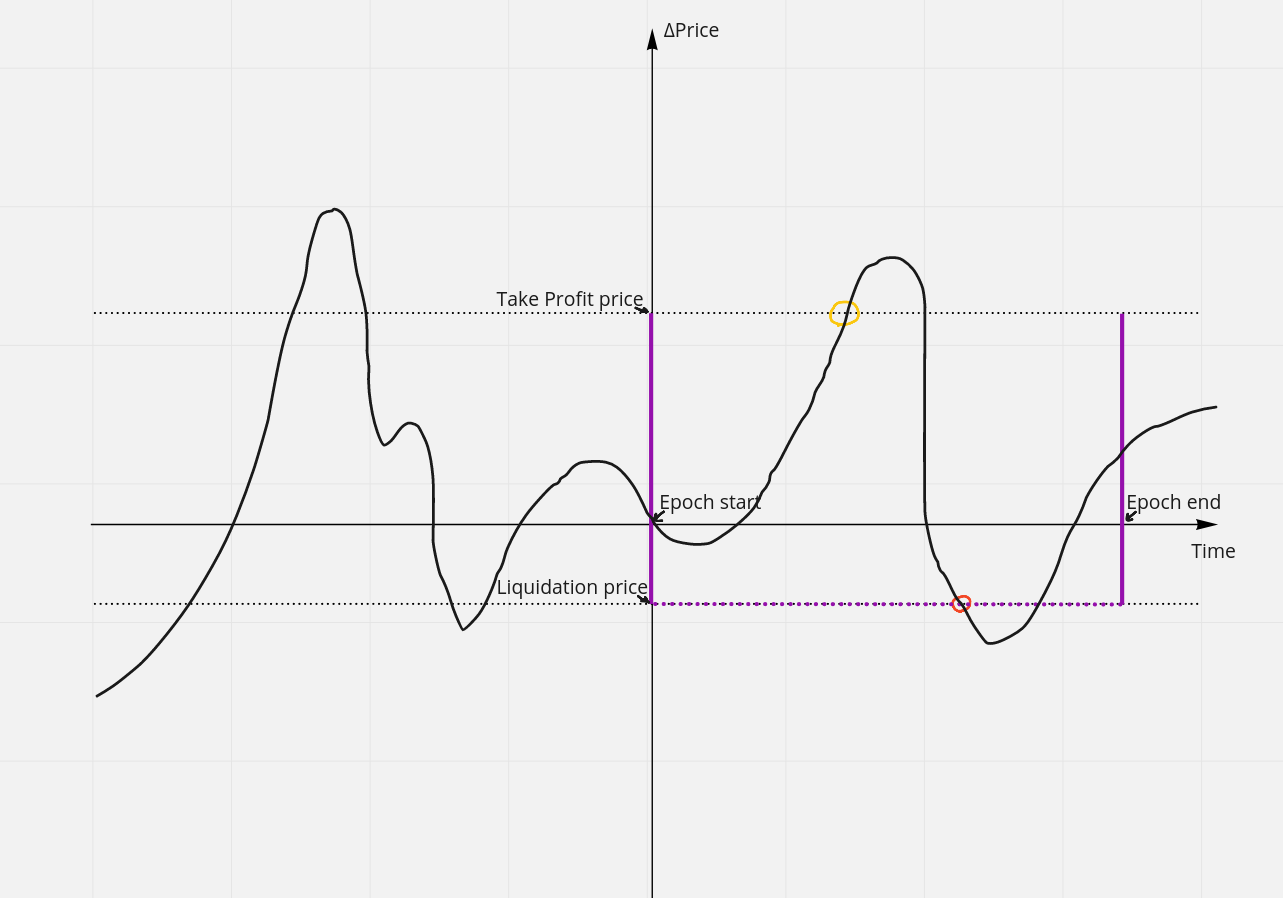
- X axis is Time with 0 at the start of current liquifunding period.
- Y axis is from the price at liquifunding period starting timestamp.
- Take Profit price is the delta price level for the liquifunding period.
- Liquidation price is delta price level for the liquifunding period.
- Orange circle is the first time Take Profit condition was satisfied. Red circle is the first time Liquidation condition was satisfied. In this case, the position should settle at Take Profit price, because it happened earlier.
The purple rectangular area is the area in question. At the end of the liquifunding period (see Section 8 for a precise definition of the time of execution), when the funding payments and borrow fee payments for that duration are made, a question needs to be answered:
- Has the price intersected either the Take Profit or Liquidation price levels and, if so, which was first and at what timestamp?
One way to answer this question is to store price feed data in a data structure that can answer:
- What is the first element of the data series that is greater (or lower) than a specific value?
That data structure must also support fast appending of new data points.
Fortunately, common blockchain storage mechanisms allow for gas-efficient querying of values. In particular, CosmWasm's de-facto standard storage library, cw-storage-plus, provides a Map data structure with a range method that allows us to find the first value before or after a given cut-off point, with gas costs being constant, or complexity. Similarly, appending new data to this data structure is also .
7.3. Liquidation and fee settling at end of liquifunding period
For a specific position , the relevant period of time for which liquidatability and fee payments are made is defined as the intersection of the lifetime of the position and the liquifunding period.
Liquidatability is checked over . If the position became liquidatable for the first time at , the position is settled with the price at . However, the fee rates are paid over the whole time period , and the delta neutrality fee is paid using the DNF rate at .
This is because the position is actually settled at a time . All the other positions and LPs may have been profiting from paying funding and borrow fee rates over the whole duration , and have been contributing to the protocol’s net notional size and utilization ratio .
In case the position has not been liquidatable over , funding payment and borrow fee payments are made for the position , and all the relevant variables for that position , , , , are updated as explained in Sections 4 and 7.1.
7.4. External bots and blockchain congestion problem
An external bot (also referred to as a crank bot) is required to execute fee payments at regular intervals.
All positions are guaranteed to be well-funded to payout fees only if the external bot checks in regularly for each position. However, the bot mechanism is fallible due to server crashes, blockchain congestion, etc., and might miss execution for a period of time.
It would be unsatisfying to build a model that gives such strong guarantees, only to break them due to fees over blockchain congestion. An easy patch solution would be to increase margin collateral to cover a longer period of time.
However, in that case, the guarantee would lose its mathematical certainty and would have a caveat: potentially unbounded bad debt due to an unbounded period of time to clean up liquidated positions that are incurring fees.
The solution, described in Section 8, is to have an internal queue that tracks work that needs to be done for every price point. This allows the protocol to “retroactively” settle fees as work items are popped from the queue. This allows Well-funded Perps to keep the well-funded guarantee even in congestion scenarios of unbound but finite length.
8. State Staleness and Cranking
The protocol has several types of upkeep workloads that need to be be executed outside of user messages. These include closing positions that have either hit their liquidation or take profit price, settling outstanding funding and borrow fees, and settling price exposure.
8.1. Settling outstanding fees
All open positions have a liquidation margin which is defined to be enough for that position to pay the maximum possible fees (at their caps) over a specified period of time. This period of time is the sum of two protocol parameters: liquifunding period and the staleness time. External bots are responsible for querying at frequent, regular intervals to check if there is any work to be done, and if so, triggering the fee settlement for each position.
If cranking is not performed in time, the protocol enters a stale state. During a stale state, open, close and update messages are disallowed. This gives the protocol time to adjust by funding or liquidating positions which are not funded for that point in time before they incur higher funding payment PnL than the collateral locked in the positions.
Before a position is closed or updated, it always pays outstanding fees. This ensures that the position will pay from the timestamp it was opened until the timestamp it was closed.
8.2. Liquidating positions
For each new price update in the protocol, there may be some positions that have hit their liquidation or take profit price. All open positions are stored so that they can be efficiently iterated over for any given price update. In addition to funding all open positions, crank messages also iterate over all the price updates to close the liquidatable positions.
When liquidating a position, the price that is used to settle the trader and LP counter-side is the one that made that position liquidatable. It's important to note that this price may be slightly in the past due to cranking being an external process. The fees are paid up until the closing timestamp (or staleness timestamp if the protocol is stale) to ensure that there are exactly the same amount of funds received and payed through funding payments.
If the last processed price update is more than staleness time in the past, the protocol also becomes stale.
8.3. Cranking
A crank message is a permissionless message that executes the aforementioned workload. The only responsibility of external bots is to check if there is any crank work available to do in the protocol and to trigger it.
Crank messages cost gas, and so they require incentivization to be attractive to execute. Rewards for successfully executing a crank message must be at least greater than the gas spent on the execution. Funds used as rewards for successful cranking would be sourced from the yield fund. The upkeep cost of a position also add a condition on minimal size of a position that would be profitable for LPs to keep.
8.4. Staleness time
Timely execution of cranking messages is required for the healthy state of the protocol. If the crank is not processing work items fast enough, the protocol enters a stale state. This protects existing traders and liquidity providers by ensuring that every open position is well-funded for the full duration of their lifetime, even in the temporarily absence of cranking messages. This state should not be reached in normal conditions, and the cranking is permissionless and incentivized to increase resilience against centralized bots crashing.
To exit the stale state, crank messages need to be executed such that their workload timeline is advanced past the staleness timestamp. All funding of the positions and liquidations are done as if the block time is the staleness timestamp simulating cranking messages coming in just before the protocol became stale. This is possible because there are no trader messages executed, making these changes not retrospective relative to previous cranking and trader messages. Additionally, it ensures that positions are funded inside the funding time range.
9. Crypto denominated markets and off-chain notional
9.1. Delta-neutral staking rewards arbitrage strategy
Crypto assets with high staking rewards provide yield denominated in that crypto asset. It is possible to hedge the staked token price exposure, but the cost of the hedge is usually higher than the staking yield, making that trade unprofitable. However, if the cost was lower, it would be an arbitrage opportunity.
Since on Levana Perps it is possible to open a short position by borrowing only a part of the notional size of the trade, that hedged position could still be profitable, even if the borrow fee rate is higher than the staking yield. Borrow fee is paid on as little as 1/30th of the notional size.
The second ongoing cost to the hedged position is the funding fee rate. The more short positions that are opened, the higher the funding rate fee becomes, and this is the limiting factor on that trade.
The arbitrage would be between interest rates on debts denominated in US dollar and staking yield minus the costs to hedge, with funding rates acting as a price signal.
For example, if staking rewards on a token are 20% and arbitrageurs may source a 4% interest rate loan on US dollars/stablecoins, the borrow fee is 30%. That would make a hedged position profitable up to 20% - 4% - 30% * 1/30 = 15% funding fee rate.
9.2. Long positions staking rewards propagation as negative funding rates
Because of the attractive opportunity to hedge spot staked positions to create delta-neutral yield, there will be a persistent funding rate bias towards paying longs. This means that a reduced yield from staking rewards would be paid to long position holders on the notional size, which is the leveraged position size.
That would make the funding fee rate from the previous example leveraged up to: 10 * -15% = -150% for a 10x long position.
This gives the opportunity for long holders to not have to bypass staking rewards completely to trade on leverage.
In essence, long position holders would earn a premium to hold price exposure of the crypto asset for hedging arbitragers as funding rate fees.
9.3. Stablecoin denominated pair with off-chain notional index
For all assets native to the blockchain, there is a possibility of creating a crypto denominated pair with the notional asset being the US dollar, itself, instead of a particular stablecoin token. This removes the risk of the stablecoin depegging and bridge hack affecting the bridged version of the stablecoin.
For the bridged crypto assets like wETH or wBTC used as collateral in reverse pairs, the risk of the hack of the bridge remains, but the stablecoin depeg risk is eliminated.
Without a dependency on the notional asset being an on-chain crypto asset, there is the possibility of listing any notional index that has a corresponding reliable oracle price feed.
There is a dependency on cash-and-carries in making the liquidity provider pool roughly delta-neutral. Therefore, only notional indices that have deep liquidity in the spot market has low risks to LPs. The spot market must have a relatively cheap way to open and maintain long and short positions.
For example, it is possible to list a Gold notional index / USDC collateral asset trading pair.
This type of trading pairs allows Levana Well-funded Perps to list any notional index on any blockchain that has an on-chain stablecoin and oracle. If there is no stablecoin on the blockchain, it is still possible to list any notional index/native blockchain token. Any position in that pair can then be hedged with US / native blockchain token to remove exposure to the native blockchain token and only have exposure to the desired notional asset.
9.4. LP’s yield on crypto tokens in crypto denominated pairs
Crypto denominated Bitcoin pairs allow LPs to provide wBTC as a principal and receive in return yield that is also denominated in wBTC. That product does not include any stablecoin risks or the risk of any altcoin going bust.
The risks that LPs take are limited to protocol bug risks and Bitcoin / US dollar spot market meltdown risks. The yield is generated from leveraged traders paying a borrow fee with a risk premium.
This is the financial model of most companies providing yield on loaned crypto assets. However, LP for Levana Perps is a DeFi protocol, making it trustless and without the risks of centralized management of funds, which have materialized recently in insolvencies of companies with such a model.
Some of these companies became insolvent due to taking on risks of unrelated tokens or reusing collateral multiple times. Well-funded Perps provides a transparent and relatively simple model with a solution for the distressed market of Bitcoin and crypto lending.
Existing lending DeFi protocols are overcollateralized, which greatly reduces the meltdown risk, but it also reduces the yield of these protocols just as much.
9.5. Settlement of crypto denominated pair trading position equivalence
A reverse-direction position settlement on a crypto denominated pair is the same as settlement of a position in a stablecoin denominated pair.
Let us consider a trader who opens a position \(pos\) in a stablecoin denominated pair with:
- \(C_{pos}\) collateral.
- \(N_{pos}\) notional size.
- With leverage \(l_{pos} = \frac{N_{pos}}{C_{pos}}\cdot p_o\).
- At price \(p_o\).
- And closes it at price \(p_c\) without liquidation or take profit.
Another trader opens a reverse position pos'C_{pos'} = \frac{C_{pos}}{p_o} crypto collateral which is notional of stablecoin denominated pair.
-
\(N_{pos'} = -p_o \cdot N_{pos} + C_{pos}\) reverse notional size.
-
With leverage \(l_{pos'} = \frac{N_{pos'}}{C_{pos'}} \cdot \frac{1}{p_o} = \frac{-p_o \cdot N_{pos} + C_{pos}}{C_{pos}} \cdot p_o \cdot \frac{1}{p_o} = -\frac{N_{pos} \cdot p_o}{C_{pos}} + 1 = -l_{pos} + 1\).
-
At reverse price \(\frac{1}{p_o}\).
-
And closes it at reverse price \(\frac{1}{p_c}\).
Payouts to the traders of \(pos\) and \(pos_r\) circa fees are:
\[P_{pos} = C_{pos} + (p_c - p_o) \cdot N_{pos} = C_{pos} + p_c \cdot N_{pos} - p_o \cdot N_{pos}\] \[P_{pos'} = C_{pos'} + (\frac{1}{p_c} -\frac{1}{p_o}) \cdot N_{pos'} = \frac{C_{pos}}{p_c} - \frac{p_o \cdot N_{pos}}{p_c} + N_{pos}\]
Because payout \(P_{pos'}\) is denominated in notional asset of the stablecoin denominated pair, by applying exchange ratio \(p_c\) at close:
\[P_{pos'} \cdot p_c = C_{pos} + p_c \cdot N_{pos} - p_o \cdot N_{pos} = P_{pos}\]
This means that by opening a position in a crypto denominated pair with the same collateral value but in the notional denomination and with signed leverage \(l_{pos'} = -l_{pos} + 1\), the trader’s payout profile is exactly the same, but with some difference in fees.
10. Risks, rewards, guarantees and fee size
With the protocol mechanics defined, we will explore the risks, rewards, guarantees, and fees that different market participants can take.
Traders get a strong, well-funded guarantee on profit and fees from liquidity providers. Liquidity providers give out these guarantees to traders and receive fees as yield in return for the risk taken to the provided principal.
The risks taken by liquidity providers scale with LPs’ exposure to the notional asset, which is the opposite of the net notional position of the traders. Therefore, the protocol has to maintain the net total notional traders’ position size roughly at 0.
- Net notional is maintained with funding payments between traders (and capped delta neutrality fee, to a lesser extent).
- Funding payments attract a special arbitraging type of trader using a cash-and-carry strategy. This strategy allows traders to enter a delta-neutral position, but still earn funding payments on the protocol, by opening a balancing reverse position on the spot market.
- If that balance is not maintained, LPs’ rough delta-neutrality breaks and exposure to the notional asset is increased. That exposure may lead the LPs’ pool to experience risks in the form of a drawdown (or gain, if traders as aggregate lose).
- Because the protocol does not need to defend its treasury with aggressive fee rates, the dynamic fee rate caps can be set significantly lower than on other perps protocols.
Another balance of the utilization ratio around target is maintained to keep the trader’s ability to open new positions with high capital efficiency.
- Utilization ratio is balanced by gradually increasing or decreasing the borrow fee rate.
- Borrow fee rate acts as the price at a point where demand for liquidity from traders meets the supply of that liquidity from providers.
- If the utilization ratio hits close to 100%, traders may be unable to open new positions.
All of the market participants take on risks of bugs and hacks of the protocol infrastructure:
- A bug in the implementation of the protocol.
- A hack of bridge of the collateral asset if it is a bridged asset.
- Oracle hack or downtime.
- Blockchain downtime removing the ability to execute messages for closing the position.
10.1. Well-fundedness guarantee to the trader
A well-fundedness guarantee to the trader is the unique proposition of Well-funded Perps in leveraged trading. This guarantee can be written out as an inequality on the position’s PnL$ (profit or loss, positive when the position is in profit and negative otherwise).
10.1.1. Guarantee inequality derivation
First, let’s look at \(PnL_{pos}\) has a lower bound on the time frame \(T_e\) of one liquifunding period:
\[PnL_{pos} \ge \operatorname{clamp}(\Delta p \cdot N_{pos} - s_{pos} - F_{max},\ -C_{pos},\ G_{pos})\]
The lower bound is calculated assuming the maximum possible delta neutrality fee at close, the maximum possible funding payment and the maximum possible borrow fee payment over the liquifunding period \(T_e\). Expanding the bounds from Sections 4.4.2, 4.5.2 and 7.1.2:
\[PnL_{pos} \ge \operatorname{clamp}(\Delta p \cdot |N_{pos}| - s_{cap} \cdot N_{pos} \cdot (p + \Delta p) - R_{f_{cap}} \cdot p_{max} \cdot T_e \cdot |N_{pos}| - R_{c_{cap}} \cdot T_e \cdot (G_{pos} + C_{pos}),\ -C_{pos},\ G_{pos})\]
And that can be expanded a bit further to use only the initial parameters of \(pos\) and price \(p\) into:
\[PnL_{pos} \ge \operatorname{clamp}((1 - s_{cap} \cdot \operatorname{sign}(N_{pos})) \cdot \Delta p \cdot N_{pos} - s_{cap} \cdot |N_{pos}| \cdot p - R_{f_{cap}} \cdot \max(p + \frac{G_{pos}}{N_{pos}}, p - \frac{C_{pos}}{N_{pos}}) \cdot T_e \cdot |N_{pos}| - R_{c_{cap}} \cdot T_e \cdot (G_{pos} + C_{pos}), -C_{pos},\ G_{pos})\]
The first part \((1 - s_{cap} \cdot \operatorname{sign}(N_{pos})) \cdot \Delta p \cdot N_{pos} - s_{cap} \cdot |N_{pos}| \cdot p\) is not dependent on the dynamic fees and is calculated precisely, while the second part \(R_{f_{cap}} \cdot \max(p + \frac{G_{pos}}{N_{pos}}, p - \frac{C_{pos}}{N_{pos}}) \cdot T_e \cdot |N_{pos}| + R_{c_{cap}} \cdot T_e \cdot (G_{pos} + C_{pos})\) is an upper bound on dynamic fees to be paid.
That second part does depend on intermediate values of collateral that changes due to the fees in previous liquifunding periods. This complicates precisely writing down guarantee inequality for time frames longer than one liquifunding period.
However, it can be greatly simplified if we allow ourselves the assumption that the trader withdraws any possible positive funding payments he receives for position \(pos\) at the end of each liquifunding period instead of “reinvesting” it into \(C_{pos}\).
With that assumption, the guarantee for an arbitrary amount \(n\) for a given liquifunding period is:
\[PnL_{pos} \ge \operatorname{clamp}((1 - s_{cap} \cdot \operatorname{sign}(N_{pos})) \cdot \Delta p \cdot N_{pos} - s_{cap} \cdot |N_{pos}| \cdot p - n \cdot (R_{f_{cap}} \cdot \max(p + \frac{G_{pos}}{N_{pos}}, p - \frac{C_{pos}}{N_{pos}}) \cdot T_e \cdot |N_{pos}| + R_{c_{cap}} \cdot T_e \cdot (G_{pos} + C_{pos})),\ -C_{pos},\ G_{pos})\]
10.1.2. Numerical examples of trader’s guarantee
The inequality has a lot of variables, but is not too complicated. Let us make some reasonable assumptions about the parameters of the trading pair:
- Stablecoin collateral asset.
- Delta neutrality cap \(s_{cap}\) is at \(0.5%\).
- Liquifunding period length \(T_e\) is 1 hour.
- Funding rate cap \(R_{f_{cap}}\) is at \(30%\) annualized.
- Borrow fee cap \(R_{c_{cap}}\) is at \(30%\) annualized.
And look at a couple of position examples:
-
Conservative longish-term bull \(pos_1\) is a \(2\times\) long position with \(10\times\)counter-side collateral leverage opened for 1 month with \($100\) in initial position value.
If price \(p\) increased by \(20%\), \(pos_1\) is guaranteed to close with profit of at least \($11.57\). It is quite a bit less than perfect \($20\) of profit.
However, it is important to remember that this simulates the worst case scenario of an unrealistic unbalancing state of the protocol staying that way for the whole month. It includes only long positions being open, without any cash-and-carries, and without any new liquidity supply attracted by sky-high yields.
The trader was able to profit even in a worst-case scenario, despite not checking his position for a month and the trading pair being completely broken for all that time, because of a well-funded guarantee.
-
Short-term \(10\times\) leverage short position \(pos_2\) with \(1\times\) counter-side leverage (to allow for huge max gains) targeting the top of the notional asset bursting and quickly going down to \(0\) in a complete meltdown. The position is opened for 1 week and has an initial value of \($100\).
If the trader was able to open that position (meaning that liquidity providers did not see the meltdown coming) and timed the burst with 1 week precision, and if the price went down by \(99%\) in that period of time, the trader would get \($982.04\) in profit, just \(\approx $8\) shy of theoretically perfect \($990.00\).
10.1.3. Trader’s guarantee visualized on a payout chart
The guarantee can be visualized on a payout chart of the position at Open (red dashed line):
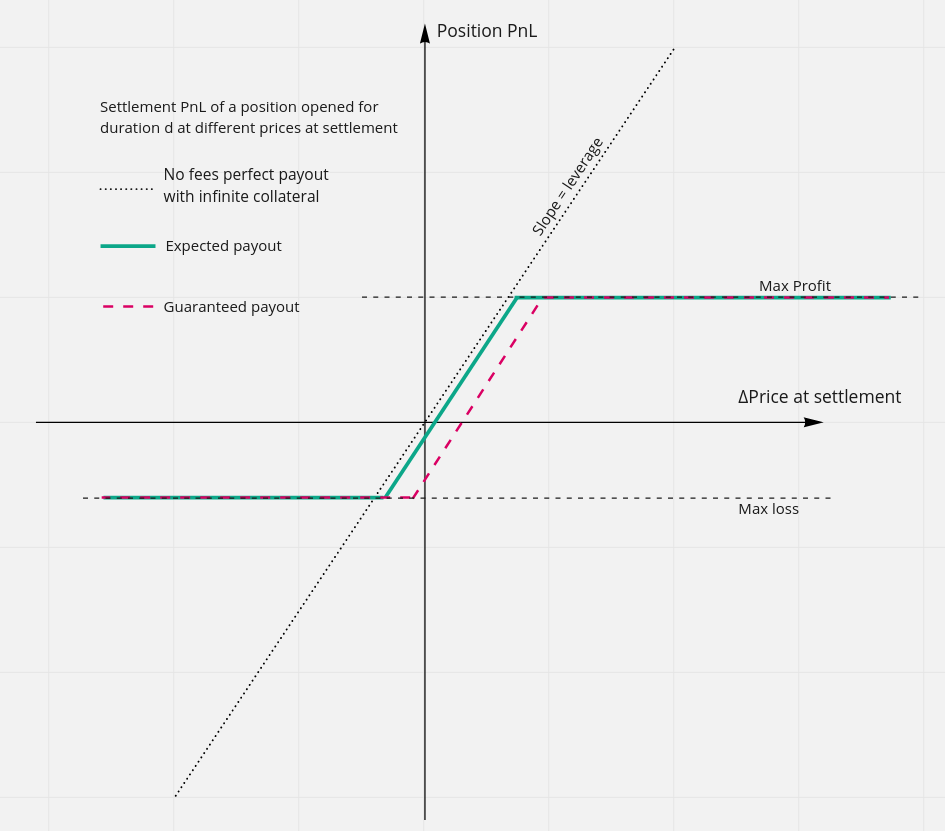
The \(X\) axis is the \(\Delta p\) and \(Y\) axis is the position’s \(PnL\) after a specified period of time.
The sloped dotted line is the \(PnL\) of the position in a perfect world with \(0\) fees of any kind and no liquidation or take profit prices.
Two horizontal lines are the max loss and max profit possible, achieved at liquidation or take profit prices of the position.
The green line is the expected \(PnL\) of the position in the business-as-usual scenario. See Section 10.3 for numerical examples.
And lastly, the red line is the trader’s guaranteed payout.
At \(\Delta p = 0\), perfect \(PnL\) is also \(0\). The expected payout is a bit shy of \(0\) because of the fees, and the guaranteed \(PnL\) is quite a bit lower at the lower bound for the worst-case market conditions scenario.
The slope of the red dashed line is just a little bit gentler than that of the perfect dotted line, with a ratio of \(1 : (1-s_{cap})\) between the slopes. \(1-s_{cap} = 0.995\) for the default delta neutrality cap, so the lines have a very similar slope in practice.
10.1.4. Risk-reward profile for traders
The purpose of opening a position is to gain exposure to the notional asset. For guaranteed exposure, traders pay fees. The exposure is the reward to the trader, while the only market condition risk that the trader takes on is the fees increasing from the expected fees up to respective caps, the magnitude of which was estimated.
This gives traders a clear framework to compare rewards and risks in order to make informed decisions. The relatively small magnitude of the effect of market risks on traders’ \(PnL\) should make Well-funded Perps very dependable, even in bad market conditions.
10.2. Risks and risk-premium for LPs
LP and xLP tokens minted to liquidity providers represent a share of the LP pool and give the owner address the right to withdraw a pro-rata ratio of funds from the Yield fund that were collected during the time that the tokens were held.
The Yield fund portion that an LP is eligible to withdraw cannot be decreased, so it is not at risk. The principal in the LP pool, on the other hand, has a risk of impairment (as well as a chance to increase). The LP pool takes a net counter-position to all traders, including arbitrage bots.
The funding payment mechanism attracts arbitrage traders who bring the LP pool into rough delta-neutrality, significantly decreasing LPs’ exposure to the notional asset. This dynamic may break if the spot market of the trading pair becomes illiquid, putting arbitrage trades at risk. This is why a meltdown or a melt-up is the main risk to LPs. LPs would experience a large drawdown to their principal if:
- The spot market becomes illiquid, putting arbitrage profitability at risk.
- The price of the notional asset in the collateral asset moves by a significant amount.
- The price moved in the direction benefiting most of the open interest in the trading pair.
10.2.1. Risks to LPs in a liquid market
Even in a liquid market with arbitrage bots active, a persistent slight delta non-neutrality is expected. Arbitrage bots will balance open interest up to a point of minimal profitability, but no further, leaving some non-zero funding and some delta non-neutrality.
The magnitude of that persistent non-neutrality can be estimated as \(\frac{R_{f}}{K_f} \cdot \frac{\sum |N| \cdot p}{V_{\operatorname{LP}} + V_{\operatorname{xLP}}}\) — This is the funding rate divided by funding rates sensitivity and multiplied by total counter-side leverage. That non-neutrality, multiplied by the trading pair price volatility, would be the price risk that LPs take. The risk premium for that is expected to be included in the borrow fee rate.
10.2.2. Risks to LPs in an illiquid meltdown
In an illiquid market, when spreads increase, sensitivity skyrockets and liquidity is withdrawn. In the worst case scenario, in a total market meltdown, usual assumptions about arbitrage keeping the notional interest balance may break.
More specifically, if the delta neutrality fee on the spot market risks become greater than the profits from arbitrage, rational actors stop doing arbitrage. This leads to net notional interest moving away from a delta-neutral state, which on its own is not an impairment, but brings about an increase of market price exposure risks to LPs.
10.2.3. Inability to withdraw locked liquidity
In an illiquid market or when borrow fee is increasing, there is a risk of not being able to withdraw the provided liquidity in a timely manner, because all of it is locked in the trades. In this case, the borrow fee rate would be gradually increasing to attract more unlocked liquidity.
10.2.4. Risk premium for providing liquidity
All of these risks are assessed by liquidity providers. From the emergent behavior of LPs and traders, a fair borrow fee would be found, which includes risk premiums for unconditionally entering counter-positions and taking risks of the market going illiquid.
10.3. Expected fees estimation
In Sections 10.1 and 10.2, the guarantees and risks of the worst case scenario for traders and LPs were shown. Let us now explore the expected fee rates of a balanced protocol.
Trading pairs with an asset that allows for high staking yield in that asset have a persistent bias of funding rates being paid to longs because of the arbitrage opportunities described in Section 9. Funding rates estimation is derived from that arbitrage profitability. Other trading pairs will have funding rates around zero. There, funding rates are derived with the usual cash-and-carry strategy profitability.
Borrow fee is derived from estimating the risk premiums that needs to be covered for LP to become attractive.
10.3.1. Expected fees derivation for assets without staking
Funding rates will be set such that performing a cash-and-carry strategy would yield a low profit.
Borrow fee rates will be set such that they covers all risk, including risk-premiums, and also the risk-free yield on the collateral.
Cash-and-carry trade having profit margin \(M\):
\[ Payout_{c\&c} = \overline{R_f \cdot p} \cdot N \approx \overline{R_f} \cdot \frac{L_{max}}{1+L_{max}} \cdot C \]
\[ Payout_{c\&c} = (1 + M) \cdot Cost_{c\&c} \]
\[ Cost_{c\&c} = Fee_{trading} + \overline{R_c} \cdot \frac{C}{1+L_{max}} + R_{loan} \cdot \frac{L_{max}}{1+L_{max}}\cdot C - s_{c\&c} \]
\[ Fee_{trading} = Fee_N \cdot n \cdot \frac{L_{max}}{1+L_{max}} \cdot C + \frac{1}{1+L_{max}} \cdot Fee_G \approx n \cdot Fee_N \cdot C \]
\[ s_{c\&c} > 0 \]
\[ Cost_{c\&c} \approx C \cdot (Fee_N \cdot n + \frac{\overline{R_c}}{1+L_{max}} + \frac{L_{max}}{1+L_{max}} \cdot R_{loan}) \]
\[ \overline{R_f} \approx (1+M) \cdot (Fee_N \cdot n \cdot \frac{1+L_{max}}{L_{max}} + \frac{\overline{R_c}}{L_{max}} + R_{loan}) \]
Where:
- \(n\) — expected number of popularity of short/long open interest reversals per year.
The borrow fee as yield that providers will demand to cover:
- The risk free rate that LPs pass up by locking collateral with Perps instead of other risk-less places, such as US treasuries for USD or overcollateralized loans.
- The risks that LPs would collectively ascribe to a market meltdown, multiplied by expected drawdown in the notional asset as illiquidity risk.
- The risks of bugs or bridge hacks, multiplied by 100% drawdown in that scenario.
- Compensation for the persistent delta neutrality ratio bias. The compensation is the delta non-neutrality multiplied by the notional asset volatility.
\[ \overline{R_c} \approx (R_{risk\_free} + R_{illiquidity} + R_{bug} + \frac{\overline{|R_f|}}{K_f} \cdot \sigma_N - R_{trading\_fees}) \cdot \frac{1}{1 - Y_{DAO}} \]
Where
- \(Y_{DAO}\) is the flat percentage of the Yield fund that DAO gets as profits.
- \(\sigma_N\) is the volatility of the notional asset.
\[ \overline{R_f} \approx (1+M) \cdot (Fee_N \cdot n \cdot \frac{1+L_{max}}{L_{max}} + R_{loan})+ \frac{(1+M)}{L_{max}}\cdot\overline{R_c} \]
\[ \overline{R_c} \approx (R_{risk\_free} + R_{illiquidity} + R_{bug} - R_{trading\_fees}) \cdot \frac{1}{1 - Y_{DAO}} + \frac{\sigma_N}{K_f \cdot (1-Y_{DAO})} \cdot \overline{|R_f|} \]
This is a system of two linear equations with two variables. It can be solved after making assumptions on all the parameters and all the market conditions.
10.3.2. Numerical fee estimations for assets without staking
Assuming these parameters for a USD/wBTC trading pair:
- \(M=40%\) profit margin for cash and carries.
- \(n=12\) cash and carry trades per year.
- \(Fee_N = 0.05%\) trading fees on notional size.
- \(L_{max} = 30\) max leverage.
- \(R_{loan} = 4.5%\) cash and carries being able to loan unlimited amount of collateral asset at that interest rate.
- \(R_{risk\_free} = 3.5%\) risk-free return on collateral asset.
- \(R_{illiquidity} = 3%\) probability of the notional asset spot market going illiquid per year multiplied by the size of the illiquid price move.
- \(R_{bug} = 3%\) probability of a catastrophic bug / exploit in the infrastructure and the protocol.
- \(R_{trading\_fees} = 5%\) expected LP yield from fees. Hard to estimate without knowledge of the total volume to open interest ratio.
- \(\sigma_N = 120%\) annualized volatility of the notional asset.
- \(K_f = 5\) sensitivity of the funding rates.
- \(Y_{DAO} = 10%\) part of Yield fund as profit for the DAO.
Gives:
- \(\overline{R_f} = 7.5%\) expected annualized funding rate.
- \(\overline{R_c} = 7.0%\) expected annualized borrow fee rate.
10.3.3. Expected fees derivation for assets with high staking yield
For borrowing USD for \(R_{loan}\) and staking the collateral asset for a higher \(R_{stake}\):
\[ R_{stake} \cdot \frac{L_{max}}{1+L_{max}} \cdot C - R_T \cdot C = \overline{R_f} \cdot \frac{L_{max}}{1+L_{max}} \cdot C + Fee_{trading} \cdot n \cdot \frac{L_{max}}{1+L_{max}} \cdot C + \overline{R_c} \cdot \frac{1}{1+L_{max}} \cdot C + R_{loan} \cdot C \]
\[ R_{stake} - R_T \cdot \frac{1 + L_{max}}{L_{max}} = \overline{R_f} + Fee_{trading} \cdot n + \frac{\overline{R_c}}{L_{max}} + \frac{(1+L_{max})\cdot R_{loan}}{L_{max}} \]
\[ \overline{R_f} = R_{stake} - R_T \cdot \frac{1 + L_{max}}{L_{max}} - Fee_{trading} \cdot n - \frac{(1+L_{max})\cdot R_{loan}}{L_{max}} - \frac{\overline{R_c}}{L_{max}} \]
Borrow fee is calculated the same way:
\[ \overline{R_c} \approx (R_{risk\_free} + R_{illiquidity} + R_{bug} + \frac{\overline{|R_f|}}{K_f} \cdot \sigma_N - R_{trading\_fees}) \cdot \frac{1}{1 - Y_{DAO}} \]
10.3.4. Numerical fee estimations for assets with high staking yield
Assuming these parameters for a USD/OSMO trading pair, estimated from OSMO staking with validators for 26% yield:
- \(Y_{target}=5%\) profit margin for arbitragers between spot staking and short Perps hedging.
- \(n=12\) cash and carry trades per year.
- \(Fee_N = 0.05%\) trading fees on notional size.
- \(L_{max} = 30\) max leverage.
- \(R_{loan} = 4%\) cash and carries being able to loan unlimited amount of collateral asset at that interest rate.
- \(R_{risk\_free} = 26%\) risk-free return on collateral asset.
- \(R_{illiquidity} = 5%\) probability of the notional asset spot market going illiquid per year multiplied by the size of the illiquid price move.
- \(R_{bug} = 3%\) probability of a catastrophic bug / exploit in the infrastructure and the protocol.
- \(R_{trading\_fees} = 10%\) expected LP yield from fees. Hard to estimate without knowledge of the total volume to open interest ratio.
- \(\sigma_N = 200%\) annualized volatility of the notional asset.
- \(K_f = 5\) sensitivity of the funding rates.
- \(Y_{DAO} = 10%\) part of Yield fund as profit for the DAO.
Gives:
- \(\overline{R_f} = -19.3%\) expected annualized funding rate — long position holders are estimated to get that rate paid on their leveraged up position size.
- \(\overline{R_c} = 35%\) expected annualized borrow fee rate on counter-side collateral.
Total fees paid or received by long position holders as an APR from the collateral used to open the position:
| Total fees for longs | 2x | 5x | 10x | 30x |
|---|---|---|---|---|
| Levana - OSMO Uncapped | 15.75% | 63.01% | 141.77% | 456.80% |
| Levana - OSMO 5x max gains | 5.63% | -7.79% | -70.63% | -422.65% |
| Levana - OSMO 10x max gains | 9.85% | 15.81% | -17.53% | -313.11% |
Where a negative number indicates a total negative fees, paying the holder of the long position.
Levana Well-funded Perps is a leveraged spot-price well-funded collateral-settled perpetual swaps protocol. It introduces a novel way to delineate risk between market participants. The incentive structure offers a risk premium to liquidity providers who take on the spot market illiquidity risk.
- Traders get strong guarantees for settlement in any future market conditions with a very low liquidation margin ratio.
- Liquidity Providers receive roughly delta-neutral yield for taking on spot market meltdown risk. That yield is found in a free market of supply and demand for liquidity to be used as collateral.
- The protocol does not require a risk fund, and DAO Treasury has no insolvency risk.
The absence of native price discovery in spot-price settled perps is addressed by introducing a Capped Delta Neutrality Fee mechanism.
Trader FAQs
- The Osmosis epoch
- Delta Neutrality Fee and DNF tax
- Price slippage
- Leverage Change over time
- No Liquidation Penalties
The Osmosis epoch
The Osmosis chain has a daily Epoch. This is a period of time when the chain calculates rewards for AMM users. During this period of time, no new transactions can land on chain. Also, at the time of writing, there are known issues with the Osmosis codebase, and the epoch can trigger node crashes after it completes. The end results of this is that, for about 15 minutes every day, it is difficult or impossible to get new transactions to land on chain.
At the time of writing, the Epoch occurs daily at 17:16 UTC. (You can check out our querier endpoint for next Epoch for up-to-date information.) The Levana Perps UI will display a banner counting down to the Epoch before it occurs, and will continue to show the banner afterwards until it can confirm that Epoch processing has finished. Unfortunately, even at that point, there may still be some remaining transaction downtime until all nodes finish process and recover from any crashes that may occur.
It's important to note that, as a result of this period, some triggers will either not fire at all or may fire at an unexpected price point. This is because during this downtime, finer grained price updates will not come through. Instead, there will be a price jump from the last update before the Epoch until transactions begin processing again.
This is an ongoing issue that the Levana team is working on in tandem with the Osmosis team. The goal is to both resolve the node crashing issues, and to minimize the length of time that the Epoch lasts.
Delta Neutrality Fee and DNF tax
Before understanding Delta Neutrality Fee and its rate, it would be helpful to understand the concept of Delta Neutrality.
Delta neutrality is a state where the total notional value of long positions is equal to the total notional value of short positions. This is important for two reasons:
-
It protects liquidity providers (LPs): LPs provide the collateral that is used to support perpetual swap positions. If the protocol is not delta neutral, this can lead to a situation where LPs are exposed to significant price risk. The delta neutrality fee helps to mitigate this risk by incentivizing traders to open positions that move the protocol towards delta neutral.
-
Ensures fair and efficient market: When the protocol is delta neutral, it means that traders are paying a fair price for the liquidity that they are using. This can help to prevent market manipulation and ensure that the protocol is a good place to trade perpetual swaps.
In Levana, the delta neutrality fee is a mechanism that aims to keep the protocol close to delta neutral. The total DNF fee you will be charged depends on these factors:
- Current Spot Price
- Net notional value: Refers to the total value of the underlying asset
- Notional delta value: The amount of change that would occur to the net notional value when you open or close a position.
- Fee cap: A fee cap acts as a safeguard, limiting the maximum fee that can be charged in any situation, including extreme market volatility.
- Sensitivity parameter: Parameter denoting the price elasiticity of the spot market.
- Liquidation margin factor: Applicable only when updating or closing the position.
You can read more details about the calculations in the whitepaper.
When opening a position in Levana, the "Delta Neutrality Fee" (DNF) reflects the total impact of the position on the protocol's delta neutrality. This includes:
- DNF paid/received on opening: This is the immediate fee charged or credited based on the position's direction and size.
- DNF that would be paid/received upon closing: This represents the estimated future fee if the position were closed right after opening.
Because of this, DNF fee will always be positive when opening a position. This ensures traders contribute to delta neutrality even if the position is closed immediately.
As market conditions change, the DNF may flip from positive to negative, meaning the trader receives this fee for their contribution to delta neutrality.
DNF Tax Rates
The DNF tax is set particularly high for the OSMO_USD market (50%)
and some other low liquidity markets. This decision stems from the
October attack on the LP pool for OSMO_USD, which we disclosed in
this blog post. For ATOM_USD market it is set to a more
reasonable 25%.
Viewing DNF for Open Positions
The DNF for an already opened position can be viewed in the Open Positions list. You can find the "+" button near the total fees paid
by the position, you may need to scroll right for that.

You can click that button to view the fees. It will be the same as shown when opening the position and it will change as the market's net notional value and the spot price changes.
Price slippage
Quick fix: if you've hit this page because you received a price slippage error on the frontend, normally you can simply check the new entry price, confirm you're happy with it, and try again. If you continue getting price slippage errors, the market may be extremely volatile. In the overflow menu (top-right of the screen), you can go to settings and increase the price slippage tolerance to a higher value.
Explanation
Price slippage is a mechanism built into many DeFi protocols. It provides a defense for users against price movements hurting their trades. For example, with Levana Perps, consider a situation where you want to open a long position on an asset. You're on the Perps site, and you see an entry price of $10. This is a value queried in many cases from an off-chain price oracle with price updates coming through at a sub-second level. You decide that $10 is a good entry price for a long position, so you enter your position details, check the price one more time, and click "open long." After approving the message in your wallet, the transaction lands on chain, and you have a new long position.
You might expect that the entry price will be exactly $10. After all, that's what you saw in the web interface. However, this can't be guaranteed. In the time between your web browser fetching the $10 price point and your transaction eventually landing on chain, there have been a number of delays:
- Normal network latency between your browser and the price oracle server
- Time spent approving the transaction (which can be significant with hardware wallets in particular)
- Transaction settlement time: the time during which your transaction is waiting to be included in a block
In that time period, it's entirely possible, and in fact likely, that a new price point will become available from the oracle and submitted to the Levana Perps market contract. Taking an extreme example, suppose the price jumped to $15. This would mean (1) you missed out on a significant amount of price movement in your favor, reducing your profits, and (2) you're exposed to significantly more risk in your position, since any movement below $15 will now be a loss.
Price slippage is the safety mechanism that prevents this from happening. When you submit a transaction to the chain, you indicate the price you are trying to use as current price, and a slippage factor. For ease of math, let's say the slippage value was 5%. (The default is much smaller at 0.5%.) When you try to open your long, the frontend will tell the smart contract "the current price is $10 and I will only allow the price to move against me by 5%." If, when your transaction lands on-chain, the current price has moved more than 5% (to over $10.50), the contract will reject the position, since it may harm you.
The usual solution to a price slippage error is to try again, assuming you're still happy with the current price. If you continuously get price slippage errors, there are two likely causes:
- Extreme market volitility, where the price is moving so quickly that you can't snag the right entry price. For this case, increase the price slippage tolerance in the settings menu can be the right solution, assuming you're comfortable with the higher risk involved.
- This could also be a frontend calculation bug (see next section), where the calculated price is incorrect. This will usually display as getting a price slippage error before approving the transaction in your wallet. If you see this happen multiple times in a row, please open a support issue.
Note that price slippage applies to opening, updating, and closing a position.
DNF (Delta Neutrality Fee)
One further complication in price slippage. An important stability mechanism in Levana Perps is the Delta Neutrality Fee, which encourages a balanced protocol and helps prevent spot price manipulation attacks from succeeding. In practice, the DNF ends up acting as a modifier to the entry price. If you open a long position when the market is overly long, it is conceptually similar to having a higher entry price. (The reverse is true too, which is part of why opening unpopular positions can be a successful trading strategy.)
When setting the "current price" in the open position transaction, the frontend includes a DNF factor in the current price to account for this. Similarly, the market contract computes a DNF factor when comparing the price against the current price.
In practice, this means that in addition to extreme spot market movement, large position movements within Levana Perps can also lead to a price slippage error occurring. The same advice as above applies: you can retry the transaction assuming you're still happy with the position details. In the case of large DNF swings, you'll see an increase in your DNF fees.
Leverage Change over time
In order to understand why the position's leverage changes over time, it's important to understand the math behind the leverage calculation.
The position's notional size is calculated once when the position is opened, and it does not change over the position's lifecycle:
- notional-size: is fixed
- entry-price: is also fixed
- collateral: changes over time (more below)
This leaves us with the leverage that will have to change over time to keep the equation stable.
Position Collateral
Over time, and as the market moves and fees are paid, your active collateral (the available collateral after fees and price movements) will fluctuate.:
- If the market moves in your favor (e.g., the price of an asset you are long on increases), your active collateral increases, and thus, your effective leverage decreases.
- If the market moves against you, your active collateral decreases, and your effective leverage increases as your position becomes riskier.
Ongoing Fees: Additionally, ongoing fees like funding payments or borrow fees will be deducted from your active collateral, which further affects the leverage over time. Also note that funding payments can also be received by the position.
Liquifunding: Levana Perps also regularly collects the fees and checks for sufficient liquidiation margin through a process called liquifunding. During this process, the system sets aside collateral for liquidation margins and realizes the fees incurred to that point, but it doesn't have any step-wise impact on leverage.
In short, while your leverage is fixed at the moment you open a position, it changes dynamically as market conditions, fees, and price movements impact your active collateral.
No Liquidation Penalties
There are no penalties for being liquidated on Levana. If a price point hits that would mean we can't guarantee liquidity through the end of the liquifunding period, the system immediately performs a close on the trader's behalf, and all fees to that point are assessed and paid. No additional penalty is incurred.
Explainer Slides
We have a set of slides explaining how the Levana Perps platform works, available at:
https://docs.levana.finance/slides/
Audits Reports
Levana Well-Funded Perpetual Swaps
- FYEO Security Assessment v1.1
- PeckShield Security Audit Report v1.0
- FYEO Security Code Review - Deferred Execution v1.0
- FYEO Security Code Review - Governance v1.0
- FYEO Security Assessment - Ruji Perps v1.0
Introduction
Levana Perps is a perpetual swaps platform for the Cosmos ecosystem. It focuses on providing well-fundedness guarantees. Every position has locked collateral from a liquidity pool for potential gains, and positions are automatically closed when there is insufficient collateral to cover future fees. As a result of this setup, there are two primary audiences for using the Levana Perps platform:
- Traders wishing to be exposed to an asset on either a long or short position. This can include:
- Speculation
- Hedging risks
- Arbitrage opportunities
- Liquidity providers wishing to receive passive rewards on their liquidity with minimal exposure to price movements.
This tutorial will walk you through the major components of the Levana Perps API with worked examples in TypeScript. You can use any language to communicate with the Levana Perps smart contracts. We have chosen to demonstrate this with TypeScript because the CosmJs library is a well supported library. In addition to CosmJs, the Levana team also uses our own cosmos-rs library for interacting with our contracts.
We also provide a sample project in Typescript if you prefer to clone and tweak from there.
Overview of Concepts
To properly interact with Levana Perps, it's helpful to have an overall concept of the platform. We recommend reviewing our high-level overview and whitepaper documents for more details. (NOTE: not currently publicly available, we will update this document with links when ready.) But as a minimal crash course in the platform and its terminology:
- Factory Each deployment of Levana Perps has a single factory contract. This is your starting point for discovering information on each individual market.
- Market A single trading pair, with a name such as
ATOM_USD,OSMO_USDC, orETH_BTC. Each of these names is made up of two components: the base asset and the quote asset. - Base asset The asset that we are speculating on the price movement of. For example, in
ATOM_USD, we are speculating on changes of the price of ATOM. - Quote asset The asset that we are pricing the base asset in.
- Collateral asset Levana Perps supports using either the base or quote asset as collateral. For example, in the markets above, ATOM, USDC, and BTC are used as the collateral assets, respectively. As a caller of the Levana Perps API, you will need to interact with the market contract by depositing the appropriate collateral asset during different API calls.
- Liquidity Liquidity providers can deposit liquidity into the system. This liquidity will be available to traders to lock into their positions. Liquidity providers can choose to deposit in exchange for LP tokens, or they can elect to time-lock their tokens for xLP tokens. Both tokens result in rewards from the system, but xLP tokens receive a higher return.
- Position A single position open by a trader. This will be a long or a short, and will have some deposit collateral, leverage, and maximum gains. As the price moves, the active collateral on the position will go up (if the price moves in your favor) or down (if the price moves against you).
There's much more to the platform, but we'll get into more details once we're writing code.
Additional information
The following links may be useful while interacting with Levana Perps:
- High level overview
- Whitepaper
- Messages API docs
- CosmJs API docs
- CosmJs tutorial
- Platform explainer slides
List of factory contracts
We'll learn more about the factory soon. For now, we'll provide the factory contract addresses in current use
MAINNET
| Chain | Factory address | Explorer link |
|---|---|---|
| Osmosis | osmo1ssw6x553kzqher0earlkwlxasfm2stnl3ms3ma2zz4tnajxyyaaqlucd45 | Explorer link |
| Sei | sei18rdj3asllguwr6lnyu2sw8p8nut0shuj3sme27ndvvw4gakjnjqqper95h | Explorer link |
TESTNET
| Chain | Factory address | Explorer link |
|---|---|---|
| Osmosis | osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u | Explorer link |
| Sei | sei1xmpv0ledn5rv46hkyzqjdgc20yyqldlwjv66vc7u4vw5h7fadfssnks3y6 | Explorer link |
Tooling Setup
For this tutorial, we are going to use the CosmJs library from TypeScript with the Yarn package manager. We'll also use Osmosis testnet for Perps. In order to send transactions on Osmosis testnet you'll need some gas coins. You can get these by tapping the faucet within the Perps Beta UI or the Osmosis faucet
We're going to reuse the same project throughout this tutorial, so you'll only need to do this setup once.
-
Create a new directory for this tutorial
-
Within that directory, create a new
package.jsonfile with the following content:{ "name": "levana-perps-tutorial", "version": "1.0.0", "description": "Tutorial Project for Levana Perps", "main": "index.js", "license": "MIT", "dependencies": { "@cosmjs/cosmwasm-stargate": "0.32.2", "@cosmjs/stargate": "0.32.2" }, "devDependencies": { "ts-node": "^10.9.1", "typescript": "^4.4.3" }, "scripts": { "tutorial": "ts-node tutorial.ts" } } -
In the same directory, create a
tutorial.tsfile with the following content:console.log("Hello World!") -
Run
yarnto install the dependencies. -
Run
yarn tutorialto run the tutorial file.
Congratulations, you now have a basic working TypeScript file! Now let's get set up with CosmJs and Osmosis Testnet.
CosmJs, Osmosis Testnet, and Levana Perps
CosmJs code needs to run within an async function. To connect to a chain, you must provide the RPC endpoint of a blockchain node. And to interact with Levana Perps, you'll need to have the contract address of a factory contract. We'll go into more details on interacting with the factory in the next section, but for now let's start with a simple example that queries the current block height of the chain and basic metadata on the Levana Perps factory we'll be interacting with:
import { CosmWasmClient } from "@cosmjs/cosmwasm-stargate"
// Testnet factory address
const factoryAddress =
"osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
const runAll = async () => {
const client = await CosmWasmClient.connect(rpcEndpoint)
const height = await client.getHeight()
console.log(`Current height: ${height}`)
const contract = await client.getContract(factoryAddress)
console.log(JSON.stringify(contract))
}
runAll()
If you copy this code into tutorial.ts and run yarn tutorial, you should get output that looks roughly like the following:
$ yarn tutorial
yarn run v1.22.21
$ ts-node tutorial.ts
Current height: 5794578
{
"address":"osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u",
"codeId":6056,
"creator":"osmo12g96ahplpf78558cv5pyunus2m66guykt96lvc",
"admin":"osmo12g96ahplpf78558cv5pyunus2m66guykt96lvc",
"label":"Levana Perps Factory - osmobeta"
}
Now that we're able to talk to the chain, let's explore the factory.
The Factory
The factory is the central place for discovering information about the Levana Perps protocol. The first thing you'll likely want to do is discover which markets are available:
import { CosmWasmClient } from "@cosmjs/cosmwasm-stargate"
// Testnet factory address
const factoryAddress =
"osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
const runAll = async () => {
const client = await CosmWasmClient.connect(rpcEndpoint)
const markets: { markets: string[] } = await client.queryContractSmart(
factoryAddress,
{ markets: {} }
)
for (const marketId of markets.markets) {
console.log(marketId)
}
}
runAll()
This program uses the queryContractSmart to make a query against the factory smart contract. CosmWasm queries are JSON objects, where the key represents the request we want to make. In this case, we're making a request to the markets query. Running this prints out all the markets available on our factory:
$ yarn tutorial
ATOM_USD
BTC_USD
We can now use another query to get more information about the ATOM_USD market:
import { CosmWasmClient } from "@cosmjs/cosmwasm-stargate"
// Testnet factory address
const factoryAddress =
"osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
const runAll = async () => {
const client = await CosmWasmClient.connect(rpcEndpoint)
const marketInfo = await client.queryContractSmart(factoryAddress, {
market_info: { market_id: "ATOM_USD" }
})
console.log(JSON.stringify(marketInfo))
}
runAll()
We're now querying the market_info query, and providing the market_id parameter with the input ATOM_USD. This results in the output:
$ yarn tutorial
{
"market_addr":"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4",
"position_token":"osmo1kqw7lkemyqdvyfqv5lt05rfgdj72qq8lh2rwpwk8p646twlpwpsqc54m9w",
"liquidity_token_lp":"osmo142cthpwtqgsdhq9ex55fp0ya4w45a2mhff3qhg5092hauhf22f4q98x2uw",
"liquidity_token_xlp":"osmo16gg2ehrl7jz43w08vvxyq8nf933vkcsae5xuzk8hc5jvdnml672s2svsy6"
}
This query provides some information on the ATOM_USD market. For now, all we care about is the market_addr, which gives the address of the market contract we will want to interact with going forward.
Reading the API docs
It's useful to be able to look at the query message API docs and see how the Rust representation matches up with the JSON representation. For example, the factory query message looks like the following (though redacted a bit):
#![allow(unused)] fn main() { pub enum QueryMsg { Markets {}, MarketInfo { market_id: MarketId, }, } }
You can see that the Markets and MarketInfo names--known in Rust as variants--turn into the snake case versions markets and market_info in the queries above. This will be a pattern you'll see repeated throughout all queries.
The vast majority of work within Levana Perps happens with the market contract. Now that we know the basics of querying a contract and have a market contract address, it's time to start playing with the market.
If you look at the specific variant documentation, such as MarketInfo you will see the return type too, which in this case is MarketInfoResponse
Querying the Market
It's time to get familiar with the market contract itself. The market QueryMsg provides a number of different queries. But we're going to start off by looking at two queries that provide protocol-wide information:
statusprovides information on the current status of the market: configuration values, available liquidity, notional interest, and more.spot_pricegives the price at a given timestamp or, if no timestamp is provided, at the current time.
import { CosmWasmClient } from "@cosmjs/cosmwasm-stargate";
// Testnet factory address
const factoryAddress =
"osmo1ymuvx9nydujjghgxxug28w48ptzcu9ysvnynqdw78qgteafj0syq247w5u"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
const runAll = async () => {
const client = await CosmWasmClient.connect(rpcEndpoint);
const { market_addr: marketAddress } = await client.queryContractSmart(
factoryAddress,
{
market_info: { market_id: "ATOM_USD" },
}
);
const price = await client.queryContractSmart(marketAddress, {
spot_price: {},
});
console.log(JSON.stringify(price));
const status = await client.queryContractSmart(marketAddress, { status: {} });
console.log(JSON.stringify(status));
};
runAll();
This demonstrates a common theme you'll have in your own code: use the factory to get the market address, and then proceed to query that market. For brevity in the rest of the tutorial, we'll simply hard-code the market address.
Spot price
Let's look at the price data, prettied up a bit:
{
"price_notional":"0.080100999350080516",
"price_usd":"12.48423875",
"price_base":"12.48423875",
"timestamp":"1709569578000000000",
"is_notional_usd":true,
"market_type":"collateral_is_base",
}
Let's start with the market_type. Our ATOM_USD market is a collateral-is-base market, meaning that we use ATOM as the collateral asset. We'll see in later sections how to get some ATOM to experiment with and how to use it with the market contract.
The timestamp field is given in nanoseconds since the epoch. You can use any epoch converter to translate into human-readable dates; epochconverter.com is a good choice. The above timestamp comes out to Monday, March 4, 2024 16:39:51 GMT.
price_base gives the price of the base asset (ATOM) in terms of the quote asset (USD). This is the standard price you're used to seeing. price_usd gives the price of the collateral asset in terms of USD. In this market, price_usd will always give the same value, since ATOM is both the base and collateral assets, and USD is the quote asset. price_notional is the price used internally by the system. For more information on how Levana Perps handles collateral-is-base markets internally, see our collateral is base slide deck.
Status
The status response provides a lot of information, and we aren't going to look at it all right now. Let's instead start with a subset of the data:
{
"market_id":"ATOM_USD",
"base":"ATOM",
"quote":"USD",
"market_type":"collateral_is_base",
"collateral": {
"cw20": {
"addr":"osmo1g68w56vq9q0vr2mdlzp2l80j0lelnffkn7y3zhek5pavtxzznuks8wkv6k",
"decimal_places": 6
}
},
"liquidity": {
"locked":"297436.161968789588197153",
"unlocked":"90564.995625182297950879",
"total_lp":"261441.162273575907212688",
"total_xlp":"130064.659093487869092113"
},
"borrow_fee":"0.01",
"borrow_fee_lp":"0.005465354312584584",
"borrow_fee_xlp":"0.004534645687415416",
"long_funding":"-0.069789280603992498",
"short_funding":"0.067865306914332403",
"long_notional":"2659830.714669499436727636",
"short_notional":"2735236.611240979886379068",
"long_usd":"2659830.714669499436727636",
"short_usd":"2735236.611240979886379068",
}
We start off with an overview of the market metadata itself: the market ID, base and quote assets, and whether market_type is collateral_is_base or collateral_is_quote. Next we get to the collateral itself. The above data says that we're using a CW20 token contract with the given address. Levana Perps supports both CW20s and native coins as collateral assets.
Next we see the liquidity section, which provides an overview of liquidity provided to the platform. The values locked and unlocked give the total amount of collateral available in the system. locked is the total collateral currently locked in positions to guarantee solvency if a trader takes profits. unlocked represents liquidity available for traders to lock up in new positions. total_lp and total_xlp give the total number of LP and xLP tokens.
borrow_fee, long_funding, and short_funding are all ratios giving annualized rates for these values. For example, above, a trader would pay approximately 12.8% APR on any funds they borrow in a position.
long_notional and short_notional represent the long and short notional interest, or the sum of all long and short position sizes currently open. An overall goal of Levana Perps is to keep the net notional, which is net_notional = long_notional - short_notional, as close to 0 as possible. And finally, long_usd and short_usd represent the same values, but converted to USD. In our ATOM_USD market, the notional interest is already expressed in USD, so the values are the same as long_notional and short_notional. But in other markets, like stablecoin-denominated markets, this won't be the case.
We could continue querying the market, but it's much more interesting to begin interacting with it. To do that, we'll need a wallet with some funds. Let's take a detour from the code and get that set up.
Set Up a New Wallet
You can use any seed phrase generation tool to set up a new wallet. We're going to use Keplr to generate our seed phrase, since our next step will be to tap a testnet faucet within the browser. Make sure you have the Keplr browser extension installed, open the "add account" page, and choose "Create new account":
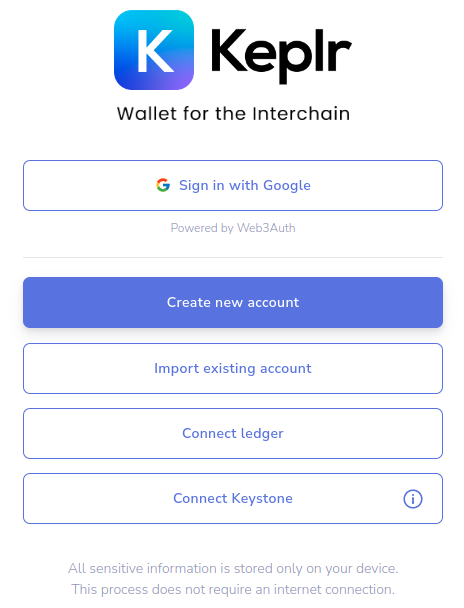
On the next screen, you'll be given your new seed phrase. Copy that string; you'll need it shortly to both finish the Keplr setup, and to continue writing our test code:
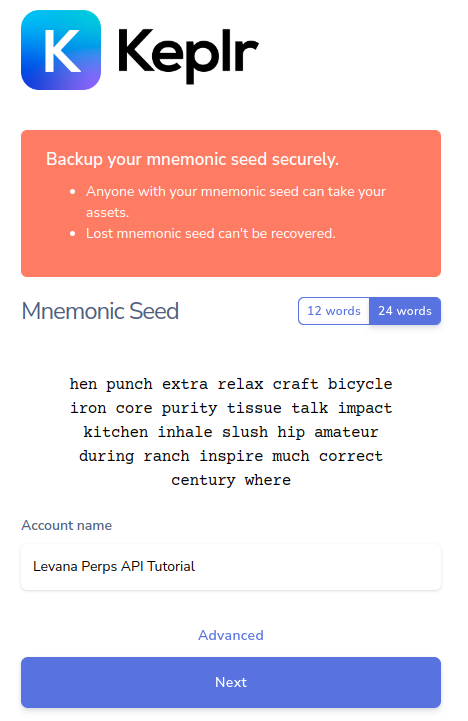
Then, on the next screen, confirm you've written down the seed phrase:
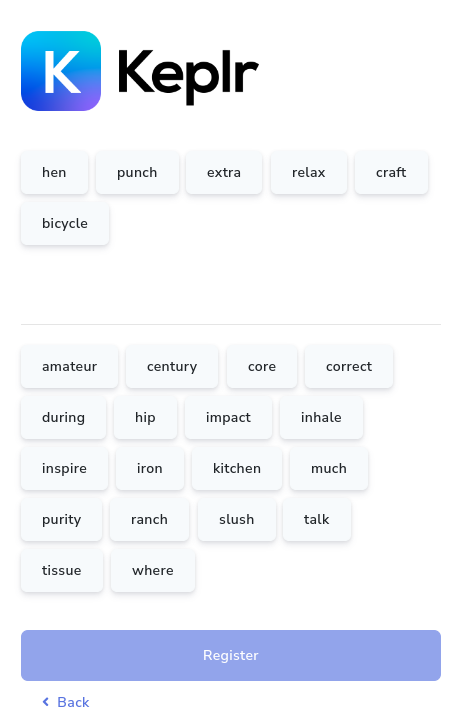
After finishing the setup, make sure you select the new wallet within the Keplr interface.
Signing Client
Now we can take our seed phrase back to our TypeScript code and create a signer and signing client:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
// Get the address of the account. This should match what you see inside Keplr
const accounts = await signer.getAccounts()
const address = accounts[0].address
console.log(`Wallet address is ${address}`)
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer
)
// And print some information about this account
const account = await client.getAccount(address)
console.log(`Account information: ${JSON.stringify(account)}`)
const balance = await client.getBalance(address, "uosmo")
console.log(`Balance is ${balance.amount}${balance.denom}`)
}
runAll()
Running this program initially resulted in the following output:
Wallet address is osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t
Account information: null
Balance is 0uosmo
The wallet address does in fact match what I see in Keplr. However, the account information is null. Until we are sent some native coins, our wallet isn't usable on the chain.
Tap the faucet
To get native coins, you can use the faucet built into the Levana Perps beta site or the Osmosis Faucet. Connect your wallet on that page and then click on the wallet address in the top right of the screen:
Once you click on the faucet button, you'll need to solve a captcha. Once that is completed, you should receive some OSMO coins for gas and ATOM tokens for collateral. Complete the captcha and then rerun the program above; you should see something like this:
Wallet address is osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t
Account information: {"address":"osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t","pubkey":null,"accountNumber":17447,"sequence":0}
Balance is 10000000uosmo
Checking CW20 collateral token balance
The getBalance method on the signing client can give us information on our native coins, but doesn't tell us anything about our CW20 balances. To do that, we need to query the CW20 contract directly. We saw this address previously in querying the market contract's status. Let's put things together and find our balance:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer
)
const status = await client.queryContractSmart(marketAddress, {
status: {}
})
const collateralAddress = status.collateral.cw20.addr
const balance = await client.queryContractSmart(collateralAddress, {
balance: { address: walletAddress }
})
console.log(balance)
}
runAll()
If you tapped the faucet via the Levana Perps beta site, then you should see something like:
{ balance: "1000000000" }
If, instead, you used the Osmosis Faucet, then you were sent gas coins but no collateral, so you will instead see:
{ balance: '0' }
The CW20 provides 6 digits of precision. You can get your token balance by dividing the value above by 10^6, or 1,000,000. This gives the 1,000 ATOM we were promised on the faucet screen.
Going forward, we'll hard-code the collateralAddress value in our program, again for brevity. But in real life code, the approach above of querying the status to find the correct collateral contract works great.
Now that we have a working wallet and some funds, we're ready to begin executing transactions against the market contract. Let's start by playing with liquidity.
Liquidity Provider
Now that we have a signing wallet, some gas coins to send transactions, and some ATOM to use as collateral, it's time to start interacting with the liquidity provider component of the API. Let's start off by querying the initial state of our wallet with the lp_info query:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
import { GasPrice } from "@cosmjs/stargate"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
// Testnet CW20 contract for ATOM collateral
const collateralAddress =
"osmo1g68w56vq9q0vr2mdlzp2l80j0lelnffkn7y3zhek5pavtxzznuks8wkv6k"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by the Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer,
// By specifying the cost of gas, we can let cosmjs determine the amount of
// gas funds to include with transactions
{ gasPrice: GasPrice.fromString("0.025uosmo") }
)
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
}
runAll()
This results in a whole bunch of zeros:
{
lp_amount: "0",
lp_collateral: "0",
xlp_amount: "0",
xlp_collateral: "0",
available_yield: "0",
available_yield_lp: "0",
available_yield_xlp: "0",
available_crank_rewards: "0",
unstaking: null,
history: { deposit: "0", deposit_usd: "0", yield: "0", yield_usd: "0" }
}
That's because we haven't actually deposited any liquidity. Let's fix that.
Depositing liquidity
Since we're using a CW20 contract for collateral, we have to use its interface for initiating a token transfer. You can read more on the CW20 spec, but the short version of what we want to do is:
- Identify the underlying message to send to the market contract
- Base64-encode that message into a simple string
- Use the CW20's
sendmethod to send a token balance and execute a method on the market contract
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
import { GasPrice } from "@cosmjs/stargate"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
// Testnet CW20 contract for ATOM collateral
const collateralAddress =
"osmo1g68w56vq9q0vr2mdlzp2l80j0lelnffkn7y3zhek5pavtxzznuks8wkv6k"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer,
// By specifying the cost of gas, we can let cosmjs determine the amount of
// gas funds to include with transactions
// this default is taken from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L21
{ gasPrice: GasPrice.fromString("0.025uosmo") }
)
// base64-encode a market ExecuteMessage, as the inner payload for the CW20 message
const msg = Buffer.from(JSON.stringify({ deposit_liquidity: {} })).toString(
"base64"
)
const execResult = await client.execute(
// Send: our wallet address
walletAddress,
// We execute this message on the collateral CW20 token
collateralAddress,
// After the CW20 receives our message, it will transfer 1 ATOM to the
// market with the deposit_liquidity message above
{ send: { contract: marketAddress, amount: "1000000", msg } },
"auto"
)
// Print out the results of executing the message: events, transaction hash, etc
console.log(execResult)
// Now get our LP info, which should be much more interesting
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
}
runAll()
After running this command, we have updated LP information:
{
lp_amount: '1.043547006279525745',
lp_collateral: '0.999999999999999999',
xlp_amount: '0',
xlp_collateral: '0',
available_yield: '0',
available_yield_lp: '0',
available_yield_xlp: '0',
available_crank_rewards: '0',
unstaking: null,
history: { deposit: '1', deposit_usd: '7.1965', yield: '0', yield_usd: '0' },
liquidity_cooldown: { at: '1695390852883629426', seconds: 3600 }
}
The lp_collateral represents the share of the collateral we have within the pool. This starts off at (approximately) 1, but will potentially change over time due to impairment. Impairment is the fact that, as traders win and lose money versus the liquidity pool, the size of the pool will change. By contrast, the lp_amount represents the amount of LP tokens our wallet has representing our collateral. This number will stay the same until we take some action to change it (which we'll see shortly).
The xlp_ field variants talk about the amount of xLP tokens, which are time-locked. We'll experiment with those shortly. The available_ fields indicate what reward amounts are available to be claimed by our wallet. Unsurprisingly, since we just deposited liquidity, we haven't earned any rewards yet. Note that the available_yield field will always be the sum of the other available_ fields.
The unstaking field is currently null, meaning we are not in the process of unstaking xLP. We'll have to get some xLP tokens before we can experiment with that.
And finally, the history field provides historical information on the total deposits and total collected yields.
Deposit to xLP
The deposit_liquidity message we used above didn't take any parameters, which led it to use its default behavior: minting new LP tokens for the deposited collateral. We can instead, however, deposit directly into xLP tokens. All we have to change is:
const msg = Buffer.from(
JSON.stringify({ deposit_liquidity: { stake_to_xlp: true } })
).toString("base64")
With this bit of code in place instead, rerunning our program now shows us both our LP and xLP balances:
{
lp_amount: '1.043547006279525745',
lp_collateral: '0.999999999999999999',
xlp_amount: '1.043547006279525745',
xlp_collateral: '0.999999999999999999',
available_yield: '0',
available_yield_lp: '0',
available_yield_xlp: '0',
available_crank_rewards: '0',
unstaking: null,
history: {
deposit: '2',
deposit_usd: '14.3980746',
yield: '0',
yield_usd: '0'
},
liquidity_cooldown: { at: '1695390852883629426', seconds: 3467 }
}
Note that we have slightly different amounts of LP and xLP tokens, and the collateral backing them is also slightly different. This is because of the impairment that occurred within the protocol between deposit for LP and depositing for xLP. Remember: the ratio between LP/xLP tokens and the underlying collateral will change over time.
Stake LP to xLP
In addition to depositing directly into xLP tokens, you can instead stake existing LP tokens into xLP tokens. This will be our first example of executing a transaction directly against the market contract, without going through the collateral CW20 contract first.
Instead of just replacing the msg payload, let's look at the entire program code again - notice that there is no base64 encoded msg payload at all, and we no longer care about the collateralAddress either:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
import { GasPrice } from "@cosmjs/stargate"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer,
// By specifying the cost of gas, we can let cosmjs determine the amount of
// gas funds to include with transactions
// this default is taken from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L21
{ gasPrice: GasPrice.fromString("0.025uosmo") }
)
const execResult = await client.execute(walletAddress, marketAddress, { stake_lp: {} }, "auto")
// Print out the results of executing the message: events, transaction hash, etc
console.log(execResult)
// Now get our LP info, which should be much more interesting
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
}
runAll()
Without any parameters, stake_lp will stake all LP tokens into xLP tokens:
{
lp_amount: '0',
lp_collateral: '0',
xlp_amount: '2.08709401255905149',
xlp_collateral: '1.999999999999999998',
available_yield: '0',
available_yield_lp: '0',
available_yield_xlp: '0',
available_crank_rewards: '0',
unstaking: null,
history: {
deposit: '2',
deposit_usd: '14.3980746',
yield: '0',
yield_usd: '0'
},
liquidity_cooldown: { at: '1695390852883629426', seconds: 3338 }
}
Alternatively, we can choose to only stake some of our LP tokens. This example will first deposit some new LP tokens and then stake some of them into xLP. Therefore, we need to base64 the payload message and use collateralAddress for the deposit part, and then a direct market contract execution for the staking part:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
import { GasPrice } from "@cosmjs/stargate"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
// Testnet CW20 contract for ATOM collateral
const collateralAddress =
"osmo1g68w56vq9q0vr2mdlzp2l80j0lelnffkn7y3zhek5pavtxzznuks8wkv6k"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer,
// By specifying the cost of gas, we can let cosmjs determine the amount of
// gas funds to include with transactions
// this default is taken from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L21
{ gasPrice: GasPrice.fromString("0.025uosmo") }
)
const msg = Buffer.from(
JSON.stringify({ deposit_liquidity: { stake_to_xlp: false } })
).toString("base64")
await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
)
console.log("After depositing LP, before staking to xLP")
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
await client.execute(
walletAddress,
marketAddress,
{ stake_lp: { amount: "0.75" } },
"auto"
)
console.log("After staking to xLP")
const lpInfo2 = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo2)
}
runAll()
With this we can see the two-step process changing our LP and xLP token balances:
After depositing LP, before staking to xLP
{
lp_amount: '4.396704079666426507',
lp_collateral: '4.999999999999999998',
xlp_amount: '1.756804235075048688',
xlp_collateral: '1.997864995281119361',
...
}
After staking to xLP
{
lp_amount: '3.646704079666426507',
lp_collateral: '4.14708837982916769',
xlp_amount: '2.506804235075048688',
xlp_collateral: '2.850776615451951669',
...
}
Which brings us to a final point: number representations. The CW20 standard always represents numbers as string-encoded integers with a certain number of decimal points. Therefore, representing a value like "2.5 ATOM" in CW20 would be "2500000". However, within the market contract we use string-encoded decimals. To represent "0.75 LP tokens", we use the string "0.75".
Unstake
xLP tokens can be unstaked into LP tokens the process happens as a linear unlock over a configurable period of time (currently: 90 days). In other words, if you unstake 90 xLP tokens today, in 5 days you'll be able to collect 5 LP tokens. You can only have one unstaking process occurring at a time, and the lp_info response's unstaking field gives information on that process. Let's start off by unstaking some xLP tokens and immediately query for the unstaking status:
await client.execute(
walletAddress,
marketAddress,
{ unstake_xlp: { amount: "2.2" } },
"auto"
)
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
Running this code shows us an unstaking process in progress:
{
lp_amount: '3.646704079666426507',
lp_collateral: '4.147007773402060011',
xlp_amount: '2.506804235075048688',
xlp_collateral: '2.850721205271022955',
available_yield: '0.00034326701085305',
available_yield_lp: '0.000039480958148038',
available_yield_xlp: '0.000303786052705012',
available_crank_rewards: '0',
unstaking: {
start: '1679304954886038378',
end: '1687080954886038378',
xlp_unstaking: '2.2',
xlp_unstaking_collateral: '2.501825457227413605',
collected: '0',
available: '0',
pending: '2.2'
},
history: { deposit: '7', deposit_usd: '85.086', yield: '0', yield_usd: '0' }
}
Notice that it is telling us: in total we are unstaking 2.2 xLP tokens. Since no time has ellapsed since we started the unstaking, none of our tokens are available as LP yet, and therefore pending still shows 2.2. However, if we query lp_info again after a small bit of time, we'll see some LP is now available:
{
lp_amount: '3.646735364074815934',
lp_collateral: '4.147132285714419282',
xlp_amount: '2.506772950666659261',
xlp_collateral: '2.850746763551560125',
available_yield: '0.000349311652552045',
available_yield_lp: '0.000042441072835686',
available_yield_xlp: '0.000306870579716359',
available_crank_rewards: '0',
unstaking: {
start: '1679304954886038378',
end: '1687080954886038378',
xlp_unstaking: '2.2',
xlp_unstaking_collateral: '2.50187911040987234',
collected: '0',
available: '0.000031284408389427',
pending: '2.199968715591610573'
},
history: { deposit: '7', deposit_usd: '85.086', yield: '0', yield_usd: '0' }
}
Notice how some of the LP has "moved" from pending into available. The way the linear unstaking process works is that the available amount is calculated lazily on each query, based on the current timestamp. However, some operations--like depositing more liquidity--will "collect" that available liquidity into the calculated field. The rule is that xlp_unstaking = collected + available + pending. We can see this in practice by explicitly collecting the unstaked LP:
await client.execute(
walletAddress,
marketAddress,
{ collect_unstaked_lp: {} },
"auto"
)
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(lpInfo)
The immediate query results in some collected LP and no available LP:
{
lp_amount: '3.646819314114995898',
lp_collateral: '4.147126593965646177',
xlp_amount: '2.506689000626479297',
xlp_collateral: '2.850581759579722187',
available_yield: '0.000388004059523683',
available_yield_lp: '0.000061392359620793',
available_yield_xlp: '0.00032661169990289',
available_crank_rewards: '0',
unstaking: {
start: '1679304954886038378',
end: '1687080954886038378',
xlp_unstaking: '2.2',
xlp_unstaking_collateral: '2.501818083339437631',
collected: '0.000115234448569391',
available: '0',
pending: '2.199884765551430609'
},
history: { deposit: '7', deposit_usd: '85.086', yield: '0', yield_usd: '0' }
}
And if we wait a bit longer and then query again, we'll see some available again as the linear unstaking process continues:
{
lp_amount: '3.646844912323768016',
lp_collateral: '4.147219276631564072',
xlp_amount: '2.506663402417707179',
xlp_collateral: '2.850596346283739866',
available_yield: '0.000397952113847755',
available_yield_lp: '0.000066266349895727',
available_yield_xlp: '0.000331685763952028',
available_crank_rewards: '0',
unstaking: {
start: '1679304954886038378',
end: '1687080954886038378',
xlp_unstaking: '2.2',
xlp_unstaking_collateral: '2.501856434244610363',
collected: '0.000115234448569391',
available: '0.000025598208772118',
pending: '2.199859167342658491'
},
history: { deposit: '7', deposit_usd: '85.086', yield: '0', yield_usd: '0' }
}
Claim rewards
As traders pay trading and borrow fees, yield is allocated to LP and xLP token holders. This yield is kept in the market contract until claimed by the liquidity providers. Claiming it is accomplished by calling the claim_yield execute message. Here is that claim in practice, together with some queries to demonstrate the change in available yield and ATOM CW20 balance:
const printValues = async () => {
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(`Available yield: ${lpInfo.available_yield}`)
const { balance } = await client.queryContractSmart(collateralAddress, {
balance: { address: walletAddress }
})
console.log(`ATOM CW20 balance: ${balance}`)
}
console.log("Before claiming")
await printValues()
await client.execute(
walletAddress,
marketAddress,
{ claim_yield: {} },
"auto"
)
console.log("After claiming")
await printValues()
And we can see the CW20 balance increase with the available yield disappearing:
Before claiming
Available yield: 0.000450582621158018
ATOM CW20 balance: 993000000
After claiming
Available yield: 0
ATOM CW20 balance: 993000452
Withdraw liquidity
LP tokens can be withdrawn into their underlying collateral. The limitation on this is that you can only withdraw unlocked liquidity (as displayed in the status query). When you specifying withdrawing, you use the amount of LP tokens you would like to withdraw:
const printValues = async () => {
const lpInfo = await client.queryContractSmart(marketAddress, {
lp_info: { liquidity_provider: walletAddress }
})
console.log(`LP tokens: ${lpInfo.lp_amount}`)
console.log(`LP token collateral: ${lpInfo.lp_collateral}`)
const { balance } = await client.queryContractSmart(collateralAddress, {
balance: { address: walletAddress }
})
console.log(`ATOM CW20 balance: ${balance}`)
}
console.log("Before withdrawing")
await printValues()
await client.execute(
walletAddress,
marketAddress,
{ withdraw_liquidity: { lp_amount: "1.2" } },
"auto"
)
console.log("After withdrawing")
await printValues()
Results in:
Before withdrawing
LP tokens: 3.647034094435032443
LP token collateral: 4.147209037218631394
ATOM CW20 balance: 993000452
After withdrawing
LP tokens: 2.447035517075706802
LP token collateral: 2.782635848207894757
ATOM CW20 balance: 994365026
Summary
Congratulations! You're now an expert at the liquidity provider portion of the API. Time to check out trading!
Trading
The trading API is all about positions. The basic lifecycle here is:
- Open a position, either:
- By opening a position directly with a market order
- Placing a limit order and waiting for the price trigger to open the position
- Query the status of the position
- If desired, update the poisition with activities such as:
- Increase position size by adding collateral
- Modifying the take profit price
- Decreasing leverage to decrease the position size
- Close the position
We'll walk through these step by step. Before getting into the API, however, it's important for you to understand the meaning of the parameters for position. You can get familiar with these from the beta web interface or by reading our documentation, specifically the slides on:
As a very terse summary for those who haven't read the above, here's an overview of the parameters needed to open a position:
- Required
- Deposit collateral: how much of the collateral asset we want to deposit. This is provided by sending the funds to the market contract (either as native coins or CW20), not an extra execute message field.
- Direction: are you trying to open a long or a short?
- Leverage: how much additional exposure are you trying to achieve?
- Take profit override: this represents the total potential profit in terms of the quote currency. This will determine how much collateral is borrowed from the liquidity pool and impact your take profit price.
- Optional
- Stop loss price
- Limit order trigger price (if placing a limit order)
- Slippage tolerance
Opening a position
Let's start off by opening a 5x leveraged long:
import { SigningCosmWasmClient } from "@cosmjs/cosmwasm-stargate"
import { DirectSecp256k1HdWallet } from "@cosmjs/proto-signing"
import { GasPrice } from "@cosmjs/stargate"
// Osmosis testnet RPC endpoint
// retrieved from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L123
const rpcEndpoint = "https://rpc.osmotest5.osmosis.zone"
// Our personal wallet seed phrase
const seedPhrase =
"hen punch extra relax craft bicycle iron core purity tissue talk impact kitchen inhale slush hip amateur during ranch inspire much correct century where"
// ATOM_USD contract address on Osmosis testnet
const marketAddress =
"osmo1kus6tmx9ggmvgg5tf88ukgxcz0ynakx38hyjy0sjgahvp7d3ut2qqtfhf4"
// Testnet CW20 contract for ATOM collateral
const collateralAddress =
"osmo1g68w56vq9q0vr2mdlzp2l80j0lelnffkn7y3zhek5pavtxzznuks8wkv6k"
const runAll = async () => {
const signer = await DirectSecp256k1HdWallet.fromMnemonic(seedPhrase, {
// This is the prefix used by Osmosis testnet
prefix: "osmo"
})
const accounts = await signer.getAccounts()
const walletAddress = accounts[0].address
const client = await SigningCosmWasmClient.connectWithSigner(
rpcEndpoint,
signer,
// By specifying the cost of gas, we can let cosmjs determine the amount of
// gas funds to include with transactions
// this default is taken from https://github.com/cosmos/chain-registry/blob/aecb225b17d1cb5a3826887735cafeb7e62934d0/testnets/osmosistestnet/chain.json#L21
{ gasPrice: GasPrice.fromString("0.025uosmo") }
)
const msg = Buffer.from(
JSON.stringify({
open_position: { leverage: "5", direction: "long", take_profit: "+Inf" },
})
).toString("base64");
const execResult = await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
);
console.log(execResult);
}
runAll()
Since we're sending funds into this contract, we use the CW20 send method and base64-encoding of the message. We use the "+Inf" to represent unbound take profit. This option is only available in collateral-is-base markets when opening a long. Besides "+Inf", we can also provide price values, regardless of the market type.
The events from the transaction above should be part of the deferred execution transaction and provide a lot of information on the actions we just took. For example, the wasm-position-open event gives us a bunch of parameters of the open position, including the position ID:
{
"type": "wasm-position-open",
"attributes": [
{
"key": "_contract_address",
"value": "osmo1g2ml4wt93w72nmdysr99ptcvjxureqggjwrdmmx3d3fn75xuf9ts57atrx"
},
{
"key": "active-collateral",
"value": "4.936079717760488888"
},
{
"key": "contract_name",
"value": "levana.finance:market"
},
{
"key": "contract_version",
"value": "0.1.0-beta.15"
},
{
"key": "counter-collateral",
"value": "20"
},
{
"key": "counter-leverage",
"value": "1.999999999999999999"
},
{
"key": "created-at",
"value": "1679889642.398222464"
},
{
"key": "deposit-collateral",
"value": "5"
},
{
"key": "deposit-collateral-usd",
"value": "56.065"
},
{
"key": "direction",
"value": "long"
},
{
"key": "levana_protocol",
"value": "perps"
},
{
"key": "leverage",
"value": "5.051798419713133722"
},
{
"key": "market-type",
"value": "collateral-base"
},
{
"key": "notional-size",
"value": "-224.260000000000001498"
},
{
"key": "notional-size-collateral",
"value": "-19.999999999999999999"
},
{
"key": "notional-size-usd",
"value": "-224.260000000000001498"
},
{
"key": "pos-id",
"value": "99"
},
{
"key": "pos-owner",
"value": "osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t"
},
{
"key": "trading-fee",
"value": "0.019999999999999999"
},
{
"key": "trading-fee-usd",
"value": "0.224259999999999988"
}
]
}
You can use this data directly, and you can store your position IDs to query up-to-date information on them. But let's see how we would find our open positions and query them directly.
Query the open position
To get a list of open positions for a wallet, we use the NFT interface. Each position within Levana Perps is treated as a unique NFT that can be transferred or sold on secondary markets. We won't be using that functionality for now, just listing the positions.
const res = await client.queryContractSmart(marketAddress, {
nft_proxy: { nft_msg: { tokens: { owner: walletAddress } } },
});
console.log(res);
You can provide all parameters supported by the CW721 spec, such as start_after and limit to enumerate through a large number of positions. In our case, we have just one position:
{ "tokens": [ '99' ] }
The position ID is internally represented as a 64-bit unsigned integer, so in order to have perfect support across systems that don't have this type, it's encoded as a string for on-the-wire messaging.
Once we have this ID, we can use it to look up the position information.
const res = await client.queryContractSmart(marketAddress, {
positions: { position_ids: ["99"] },
});
console.log(res);
position_ids supports an array of position IDs to query, and will return a JSON structure like this:
{
"positions": [
{
"owner": "osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t",
"id": "99",
"direction_to_base": "long",
"leverage": "4.991495369223277244",
"counter_leverage": "1.999999999999999999",
"created_at": "1695387960608855254",
"liquifunded_at": "1695387960608855254",
"trading_fee_collateral": "0.04",
"trading_fee_usd": "0.28838",
"funding_fee_collateral": "-0.001523571652950209",
"funding_fee_usd": "-0.011006054395435988",
"borrow_fee_collateral": "0.000020579249505979",
"borrow_fee_usd": "0.00014866142924192",
"crank_fee_collateral": "0",
"crank_fee_usd": "0",
"delta_neutrality_fee_collateral": "0.000535571339138809",
"delta_neutrality_fee_usd": "0.004049209964128253",
"deposit_collateral": "5",
"deposit_collateral_usd": "36.0475",
"active_collateral": "5.000699304454821595",
"active_collateral_usd": "36.12430597108736481",
"counter_collateral": "19.960268116609483826",
"pnl_collateral": "0.000699304454821595",
"pnl_usd": "0.07680597108736481",
"dnf_on_close_collateral": "0.013100845148444754",
"notional_size": "-144.190000000000000258",
"notional_size_in_collateral": "-19.960268116609483825",
"position_size_base": "24.960967421064305419",
"position_size_usd": "180.314305971087364816",
"liquidation_price_base": "5.811276064335014016",
"liquidation_margin": {
"borrow": "0.013663018160800488",
"funding": "0.02204896776840991",
"delta_neutrality": "0.124862826369046529",
"crank": "0.001387058741937721"
},
"take_profit_price_base": null,
"entry_price_base": "7.209500000000000012",
"next_liquifunding": "1695408222608855254",
"stale_at": "1695416760608855254",
"stop_loss_override": null,
"take_profit_override": "+Inf"
}
],
"pending_close": [],
"closed": []
}
The top level JSON structure includes three keys:
positionsare positions which are currently open and active.pending_closeare positions which need to be closed because of a liquidation, stop loss, or take profit. Once the crank runs, this position should move toclosed.closedis positions that have been fully closed. We'll see some of that output towards the end of this chapter.
For more information on the meaning of each of these fields, please see the API reference docs.
Slippage tolerance
Slippage tolerance can be used to prevent a position from opening if the price has moved significantly from the time the trader tried to open the position. Let's simulate a failure by placing a slippage parameter when trying to open a short. To cause the failure, we'll put the expected price significantly higher than the current spot price:
const msg = Buffer.from(
JSON.stringify({
open_position: {
leverage: "5",
direction: "short",
take_profit: "3.5",
slippage_assert: { price: "100", tolerance: "0.01" },
},
})
).toString("base64");
const execResult = await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
);
This program produces the output:
Error: Query failed with (6): rpc error: code = Unknown desc = failed to execute message; message index: 0: dispatch: submessages: {
"id": "slippage_assert",
"domain": "market",
"description": "Slippage is exceeding provided tolerance. Slippage is 791.99920844611191%, max tolerance is 1%. Current price: 11.209. Asserted price: 100.",
"data": null
}: execute wasm contract failed [CosmWasm/[email protected]/x/wasm/keeper/keeper.go:425] With gas wanted: '0' and gas used: '225810' : unknown request
Our message asserted that the current price is 100 USD per ATOM, while the smart contract views the current price (at time of running) as 11.209. By stating 0.01 for the tolerance parameter, we're saying that the maximum the price can deviate against the trader is 1%. Therefore, this open position is rejected.
Stop losses
When you open a position, you can set a stop loss on the position. Let's actually open a short this time, and place a stop loss at a price above the current entry price but below the liquidation price:
const msg = Buffer.from(
JSON.stringify({
open_position: {
leverage: "5",
direction: "short",
take_profit: "2.5",
slippage_assert: { price: "11.209", tolerance: "0.01" },
stop_loss_override: "11.5",
},
})
).toString("base64");
const execResult = await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
);
console.log(JSON.stringify(execResult));
Looking at the event output (which we won't show here for brevity), the position ID is "245155". We can query the open position to see the liquidation and stop loss prices:
const res = await client.queryContractSmart(marketAddress, {
positions: { position_ids: ["245155"] },
});
const pos = res.positions[0];
console.log(`Unrealized PnL: ${pos.pnl_usd}`);
console.log(`Liquidation price: ${pos.liquidation_price_base}`);
console.log(`Stop loss: ${pos.stop_loss_override}`);
console.log(`Take profit: ${pos.take_profit_override}`);
This outputs:
Unrealized PnL: -0.276837137536798332
Liquidation price: 13.055139080302147435
Stop loss: 11.5
Our position starts off with negative PnL since we had to pay fees from our collateral to open the position. Our stop loss price is exactly the 11.5 value we specified above, and our liquidation price is calculated to be about 13.06. We can modify our stop loss price if we want:
const msg = Buffer.from(
JSON.stringify({
update_position_stop_loss_price: {
id: "4854",
stop_loss: "remove",
},
})
).toString("base64");
await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
);
With that change in place, we now see our updated stop loss price:
Unrealized PnL: -0.199828868790545317
Liquidation price: 13.037564011474705624
Stop loss: null
Placing a limit order
When you open an order using the open_position API, you create a market order that uses the current spot price. You can instead place a limit order. With limit orders, you're guaranteed to get the limit price you request or better. It's also possible that the order will be cancelled if, at the time of opening, there are any issues preventing the order from being placed, such as insufficient liquidity in the liquidity pool.
The parameters for placing a limit order look very similar to placing a market order, with two differences:
- Limit orders require a
trigger_priceparameter - Limit orders do not support a
slippage_assertparameter, since you specify the entry price yourself
Let's place a short limit order by setting a trigger price above the current spot price:
const msg = Buffer.from(
JSON.stringify({
place_limit_order: {
leverage: "5",
direction: "short",
take_profit: "2.5",
trigger_price: "11.159",
},
})
).toString("base64");
const execResult = await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "5000000", msg } },
"auto"
);
console.log(JSON.stringify(execResult));
Instead of receiving a position ID, we receive an order ID in the events. The wasm-place-limit-order event from the above execution gave me:
{
"type": "wasm-place-limit-order",
"attributes": [
{
"key": "_contract_address",
"value": "osmo1g2ml4wt93w72nmdysr99ptcvjxureqggjwrdmmx3d3fn75xuf9ts57atrx"
},
{
"key": "contract_name",
"value": "levana.finance:market"
},
{
"key": "contract_version",
"value": "0.1.0-beta.15"
},
{
"key": "deposit-collateral",
"value": "4.999103621369666548"
},
{
"key": "deposit-collateral-usd",
"value": "55.770000000000000009"
},
{
"key": "direction",
"value": "short"
},
{
"key": "levana_protocol",
"value": "perps"
},
{
"key": "leverage-to-base",
"value": "-5"
},
{
"key": "market-type",
"value": "collateral-base"
},
{
"key": "order-id",
"value": "187"
},
{
"key": "pos-owner",
"value": "osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t"
},
{
"key": "trigger-price",
"value": "11.159"
}
]
}
We can use the order-id of 187 above to check the status of our limit order:
const res = await client.queryContractSmart(marketAddress, {
limit_order: { order_id: 187 },
});
console.log(JSON.stringify(res));
Resulting in:
{
"order_id": 187,
"trigger_price": "11.159",
"collateral": "4.999103621369666548",
"leverage": "5",
"direction": "short",
"stop_loss_override": null,
"take_profit_override": null
}
And if desired we can cancel our limit order:
await client.execute(
walletAddress,
marketAddress,
{ cancel_limit_order: { order_id: 187 } },
"auto"
);
Add collateral
Let's get back to our existing open positions. Levana Perps provides a lot of flexibility to update existing positions. The first update mechanism we'll look at is adding collateral. When adding collateral, you get to decide whether the position should be updated by:
- Increasing the position size, exposing you further to price movements, while keeping the leverage the same
- Decrease the leverage, reducing your risk of liquidation, but not giving you more price exposure
We can see the former with the code:
const msg = Buffer.from(
JSON.stringify({
update_position_add_collateral_impact_size: {
id: "99",
},
})
).toString("base64");
await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "1000000", msg } },
"auto"
);
And the latter with:
const msg = Buffer.from(
JSON.stringify({
update_position_add_collateral_impact_leverage: {
id: "99",
},
})
).toString("base64");
const execResult = await client.execute(
walletAddress,
collateralAddress,
{ send: { contract: marketAddress, amount: "1000000", msg } },
"auto"
);
Remove collateral
You can also choose to remove collateral, with the same decision to either decrease position size or increase leverage. This can be useful if you've experienced price movement in your favor and would like to take some profits.
Decreasing size:
await client.execute(
walletAddress,
marketAddress,
{
update_position_remove_collateral_impact_size: {
id: "99",
amount: "0.75",
},
},
"auto"
);
Increasing leverage:
const execResult = await client.execute(
walletAddress,
marketAddress,
{
update_position_remove_collateral_impact_leverage: {
id: "99",
amount: "0.75",
},
},
"auto"
);
Note that when passing in amount here, we use the decimal-encoded version of the value. 0.75 means 0.75 ATOM, or 750000uatom.
Change leverage and modify the take profit price
For our final set of updates, we can change leverage without adding or removing collateral. Updating the leverage will modify the position size (higher leverage means larger position), while modifying the take profit price will impact your take profit price and borrow fees.
await client.execute(
walletAddress,
marketAddress,
{
update_position_leverage: {
id: "99",
leverage: "15",
},
},
"auto"
);
await client.execute(
walletAddress,
marketAddress,
{
update_position_take_profit_price: {
id: "99",
price: "2.3",
},
},
"auto"
);
Closing a position
And finally, when we're done with a position, we can close it using the close_position message:
await client.execute(
walletAddress,
marketAddress,
{ close_position: { id: "99" } },
"auto"
);
Once a position is closed, we can still query it:
const res = await client.queryContractSmart(marketAddress, {
positions: { position_ids: ["99"] },
});
console.log(JSON.stringify(res));
But now that our position is closed, it will appear in the closed field instead of the positions field:
{
"positions": [],
"pending_close": [],
"closed": [
{
"owner": "osmo1g4unz9tzpdlaluqgyt0jjq5kyzuylg2a36086t",
"id": "99",
"direction_to_base": "long",
"created_at": "1679889642398222464",
"liquifunded_at": "1679898724933076589",
"trading_fee_collateral": "0.076983773508679359",
"trading_fee_usd": "0.859852989798127206",
"funding_fee_collateral": "0.000039121444204281",
"funding_fee_usd": "0.000435428475475964",
"borrow_fee_collateral": "0.000810696199482583",
"borrow_fee_usd": "0.009022695213614841",
"crank_fee_collateral": "0",
"crank_fee_usd": "0",
"delta_neutrality_fee_collateral": "0.037906133680913301",
"delta_neutrality_fee_usd": "0.425282703238582748",
"deposit_collateral": "5.5",
"active_collateral": "5.283818160624093971",
"pnl_collateral": "-0.216181839375906029",
"pnl_usd": "-2.665508418238231754",
"notional_size": "-829.985329366266828543",
"entry_price_base": "11.213",
"close_time": "1679898724933076589",
"settlement_time": "1679898724933076589",
"reason": "direct"
}
]
}
Again, you can get more information on the meaning of each of these fields by looking at the message documentation.
With all that covered, you should now be set up to begin programmatic trading with Levana Perps!
Running the crank
The crank is a mechanism within the Levana Perps market contract to handle work items that don't fit into the normal blockchain transactional paradigm. This includes, but is not limited to:
- Periodically collecting fees from users. Fee collection happens over time and is not tied to a specified user transaction, so some kind of extra mechanism needs to run these transactions.
- Liquidations and other price triggers. These actions run in response to changes in the market price, not from an immediate action the user took.
- More esoteric cases, such as resetting the LP balances in the extreme case of total liquidity pool liquidation. This handles the fact that there is an unbounded amount of computation to perform and it may need to span multiple transactions.
The common denominator here is that the crank handles core tasks that are vital to the health and stability of the platform. If fees are not collected and positions not liquidated, we can end up in an illiquid state, which violates the core premise of Levana Perps. So how does the crank get run?
Under normal circumstances, we leave cranks to a crank bot, which essentially:
- Queries the contract to determine if there's work available to be done.
- If there is work to be done, it "turns the crank."
While crank bots are ideal for this, this page documents how to manually run this process so that:
- Others can implement their own crank bots.
- If necessary, such as all crank bots being unavailable, individuals can run the crank themselves. This is key to the decentralization strategy of Levana Perps: cranking is a fully permissionless process that anyone can engage in. Furthermore, our goal is that, long term, crank fees and crank rewards will fully reimburse crankers for the gas fees they pay in cranking, making it a net-profit opportunity.
Resources
You'll need the list of factory contracts. We'll also be referencing the message API documentation. And finally, we'll use Levana's smart contract GUI for interacting with the contracts, though you can also use other approaches for interacting with the contracts.
OK, let's see how to crank!
Get the market contract
Open up the smart contract GUI, choose the network you want to query, and under "message type" choose "raw message." In the "contract address" field, enter the factory address from the list referenced above, e.g. osmo1ssw6x553kzqher0earlkwlxasfm2stnl3ms3ma2zz4tnajxyyaaqlucd45 for Osmosis. Then click on "query message."
Next, you can use the following query to list the markets available for that factory:
{"markets":{}}
At the time of writing, you'll get a response that looks like:
{
"markets": [
"ATOM_USD",
"BTC_USD",
"OSMO_USD",
"SEI_USD",
"axlETH_USD"
]
}
Next, you'll want to get information on the specific market you're trying to crank. Supposing you want to crank the ATOM market, you'll run the query:
{"market_info":{"market_id":"ATOM_USD"}}
Which will give you a result such as:
{
"market_addr": "osmo1hd7r733w49wrqnxx3daz4gy7kvdhgwsjwn28wj7msjfk4tde89aqjqhu8x",
"position_token": "osmo12dftzwa3dcuu7snpadu2ur9q8vcquuzy0ua292cupfvnj9r2qmlsp8u7hw",
"liquidity_token_lp": "osmo1kp5nhg2eqcv8zwc0ndgjj7w8pk8dzhu58jfk4q0ptfywj2m42qvqhh9dcv",
"liquidity_token_xlp": "osmo157qp6kjse4mkaw2wtrhl3a0djp6ymcgdg5vrmfk48ftsecx8pm3sc97vap",
"price_admin": "osmo1qt08s00nfgrxvpx74hvucpctsffgnr6n54lgkd6lntgcylfs4u6qy6gy0m"
}
You'll want to use the market_addr field for further interactions. Copy/paste that value (osmo1hd7r733w49wrqnxx3daz4gy7kvdhgwsjwn28wj7msjfk4tde89aqjqhu8x) into the "contract address" field.
Check for crank work
To check for crank work, you'll want to make a status query. The status query looks like this:
{"status":{}}
This will return a lot of information on the protocol, such as the config and liquidity available. However, the primary thing we care is the next_crank field. If it's null, there's no current work to be done in the crank queue. If it's anything except null, there's work to be done. Also interesting are the following fields:
"stale_liquifunding": null,
"stale_price": null,
"congested": false,
These indicate whether the protocol has reached staleness (when too much time has passed without a crank or price update) or become congested (when too many backlogged cranks are still waiting to be processed).
Assuming that there's some work on the crank queue, the next step is to execute it.
Run a crank
For the next step, click on "execute message" instead of "query message." The crank message itself is nice and simple:
{"crank":{}}
There are additional parameters you can set if you want, which are covered in the API documentation. But this message will execute up to 7 work items and send any crank rewards to the calling wallet.
And that's it! Now you too can be part of the proper functioning of the Levana Perps system.
Historical Funding Rates
$ curl 'https://indexer-mainnet.levana.finance/funding-rates?market=osmo1hd7r733w49wrqnxx3daz4gy7kvdhgwsjwn28wj7msjfk4tde89aqjqhu8x&start_date=2023-08-01&end_date=2023-08-31' | jq
Please refer to this page about how to obtain the market address.
The response contains hourly values of long and short funding rate.
[
{
"timestamp": "2023-08-31T21:00:00Z",
"long_rate": "0.41860288523718490400",
"short_rate": "-0.64021499505209033800"
},
...
]
The long_rate and short_rate are annualized APRs meaning the value 0.41 is 41% APR.
Source code
Perps contracts
| Git SHA | Code link | Checksums |
|---|---|---|
92bfa9d7265a7aec8bc2ddc5f476c179985f48d5 | Code | Checksums |
a08a140a26c1ac0f050b773e1086ca684aa4624c | Code | Checksums |
09c6ce97947a7f429ae5a807b27461396b6a1408 | Code | Checksums |
c4857a2ea087dc47a008c292a8f242c42dfa4ae7 | Code | Checksums |
98081c4648418e115906c2d960901e699b1381a9 | Code | Checksums |
ed7102d64e97931986338f82663834640d14a826 | Code | Checksums |
6d6c9eeca52fce4e5c482a724796c481fc374537 | Code | Checksums |
9cb96661a27f509d1e8bd714117184c72d4dfb93 | Code | Checksums |
1ccadfc1341288bc8e921fb2b9874810adac906b | Code | Checksums |
faa2881b21575d6859113229544046b9df878385 | Code | Checksums |
532f6673aeb398ac46847214a913148d4e09495c | Code | Checksums |
ce86c8758b2d4f4e66a1e92dd2be08be5349060a | Code | Checksums |
d2f81083b19c1cad899b4072daea25b5e989d733 | Code | Checksums |
bc5b5cddd3251668f627174a6e0c2bf78da2bc6c | Code | Checksums |
ab41b7d1bf6507cb5880ce267298d31ecd04c980 | Code | Checksums |
092eabd1d34a867a8ab42bc7f5a8c99efce484b3 | Code | Checksums |
e80e7e56b9f76b379d10276c220a62f41f9d716e | Code | Checksums |
96f0afaea94db8a66cf20c103ee4d780c01ee3eb | Code | Checksums |
0ec575544cc971c6c2d80e571f441409895482af | Code | Checksums |
Governance contract
| Git SHA | Code link | Checksums |
|---|---|---|
bc062ade5fe84251d8add32f1acb4ca2f0dcfb1e | Code | Checksums |
2d5d4df0446f00bb2f9bdf1970c2ab07ae46a3af | Code | Checksums |
License modifications
This page is intentionally left blank. In the future, it may contain updated information on Levana Perpetual Swaps software licensing.
License
Business Source License 1.1
License text copyright (c) 2017 MariaDB Corporation Ab, All Rights Reserved. "Business Source License" is a trademark of MariaDB Corporation Ab.
-----------------------------------------------------------------------------
Parameters
Licensor: Levana Foundation
Licensed Work: [Levana Perpetual Swaps]; the Licensed Work is (c) 2023 Levana Foundation
Additional Use Grant: Any uses listed and defined at: https://docs.levana.finance/license-modifications
Change Date: The earlier of July 16, 2025 or a date specified at: https://docs.levana.finance/license-modifications
Change License: GNU General Public License v2.0 or later
-----------------------------------------------------------------------------
Terms
The Licensor hereby grants you the right to copy, modify, create derivative works, redistribute, and make non-production use of the Licensed Work. The Licensor may make an Additional Use Grant, above, permitting limited production use.
Effective on the Change Date, or the fourth anniversary of the first publicly available distribution of a specific version of the Licensed Work under this License, whichever comes first, the Licensor hereby grants you rights under the terms of the Change License, and the rights granted in the paragraph above terminate.
If your use of the Licensed Work does not comply with the requirements currently in effect as described in this License, you must purchase a commercial license from the Licensor, its affiliated entities, or authorized resellers, or you must refrain from using the Licensed Work.
All copies of the original and modified Licensed Work, and derivative works of the Licensed Work, are subject to this License. This License applies separately for each version of the Licensed Work and the Change Date may vary for each version of the Licensed Work released by Licensor.
You must conspicuously display this License on each original or modified copy of the Licensed Work. If you receive the Licensed Work in original or modified form from a third party, the terms and conditions set forth in this License apply to your use of that work.
Any use of the Licensed Work in violation of this License will automatically terminate your rights under this License for the current and all other versions of the Licensed Work.
This License does not grant you any right in any trademark or logo of Licensor or its affiliates (provided that you may use a trademark or logo of Licensor as expressly required by this License).
TO THE EXTENT PERMITTED BY APPLICABLE LAW, THE LICENSED WORK IS PROVIDED ON AN "AS IS" BASIS. LICENSOR HEREBY DISCLAIMS ALL WARRANTIES AND CONDITIONS, EXPRESS OR IMPLIED, INCLUDING (WITHOUT LIMITATION) WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, NON-INFRINGEMENT, AND TITLE.
MariaDB hereby grants you permission to use this License’s text to license your works, and to refer to it using the trademark "Business Source License", as long as you comply with the Covenants of Licensor below.
-----------------------------------------------------------------------------
Covenants of Licensor
In consideration of the right to use this License’s text and the "Business Source License" name and trademark, Licensor covenants to MariaDB, and to all other recipients of the licensed work to be provided by Licensor: (i) to specify as the Change License the GPL Version 2.0 or any later version, or a license that is compatible with GPL Version 2.0 or a later version, where "compatible" means that software provided under the Change License can be included in a program with software provided under GPL Version 2.0 or a later version. Licensor may specify additional Change Licenses without limitation; (ii) to either: (a) specify an additional grant of rights to use that does not impose any additional restriction on the right granted in this License, as the Additional Use Grant; or (b) insert the text "None"; (iii) to specify a Change Date; and (iv) not to modify this License in any other way.
-----------------------------------------------------------------------------
Notice
The Business Source License (this document, or the "License") is not an Open-Source license. However, the Licensed Work will eventually be made available under an Open-Source License, as stated in this License.